2021년도에 대학교 과목으로 들었던 '기계학습' 강의를 복습 및 정리 + 추가적인 공부를 위해 이 글을 작성한다. (세종대학교 최유경 교수님 '2021 기계학습'수업)
이번 파트는 머신러닝의 꽃이자 종착역인 앙상블에 대해 알아본다. 사실 앙상블은 여러 의미를 지니고 여러 용도를 가지고 있지만, 여기서는 이전에 배웠던 지도학습의 여러 모델들을 다 같이 사용하거나 하나의 모델을 여러번 사용하여 더 좋은 결과를 얻는 방법에 관한 앙상블에 대해 알아보려 한다.
앙상블(Ensemble)
이론
앙상블이란, 여러 분류기를 하나로 연결하여 개별 분류기보다 더 좋은 일반화(generalization) 성능을 달성하는 것을 이야기한다. 즉, '여러 모델을 함께 사용하자!'의 아이디어인 것이다. 이 앙상블에는 여러 분류 알고리즘을 사용하는 다수결 투표(Majority Voting), 하나의 분류 알고리즘을 여러 번 이용하는 배깅(Bagging)과 부스팅(Boosting) 2가지로 나뉘게 된다.
1. 다수결 투표(Majority Voting)
기본적으로 의사결정나무(Decision Tree), KNN(k-Nearest Neighbor), LDA(Linear D Analysis), 로지스틱 회귀(Logistic Regression) 등 여러 학습 모델을 동시에 사용하여 각각의 모델이 예측한 결과 중 가장 많이 나온 결과를 최종 예측으로 사용한다는 개념이다. (회귀에선 모든 예측치의 평균). 즉, 여러 예측 알고리즘을 조합하여 예측 성능을 향상시키는 것에 목적을 둔다. 이에 따라 다수결 투표는 각각의 모델에 다른 데이터로 학습이 이루어지면 안되기에 동일한 학습 데이터만을 사용한다.

2. 배깅(Bagging)
배깅은 앞서 설명한 것과 같이 하나의 분류 알고리즘을 여러 번 이용하여 분류 결과를 결정한다. 또한 이는 다수결 투표와 다르게 알고리즘마다 별도의 학습 데이터를 추출(샘플링)하여 모델 구축에 사용한다. 배깅은 이 학습데이터 샘플링 시 복원 추출(중복)을 허용하는 부트스트랩(Bootstrap)을 사용하여 모델의 학습을 다수결 투표와 같이 병렬적으로 처리하게 된다.

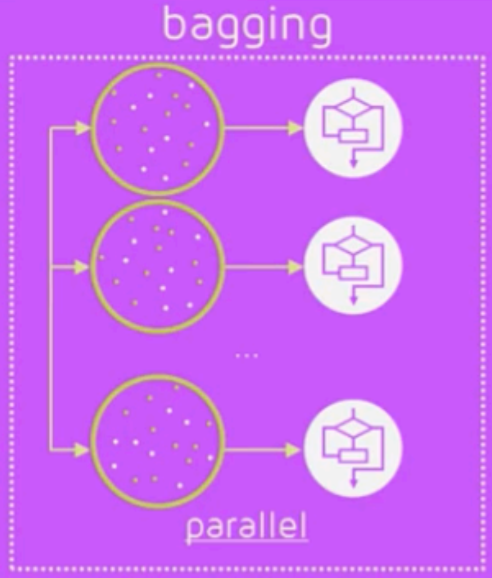
이런 배깅에는 대표적으로 이전에 설명했던 랜덤포레스트(Random Forest)가 있다.
랜덤 포레스트는 앞서 설명했던 배깅의 특징과 같이 학습 데이터를 샘플링하여 각각의 단일 분류 모델(Decision Tree)의 학습을 진행한다. 이 때의 각 Tree들은 기존의 Decision Tree에서 사용하는 불순도 알고리즘을 이용하는 것이 아닌 무작위로 예측변수를 선택하여 각 모델을 구축한다. 즉, 각각의 Tree들이 모여 결과적으로 Forest를 구축하게 되는 것이다. 이때 대상에 대한 예측을 내릴 때는 분류는 다수결 투표를 통해, 회귀는 평균화를 통해 결정하게 된다.

그렇다면 이 랜덤포레스트는 어떤 절차를 통해 분석이 진행될까? 일단 d개의 특성 변수를 가진 학습데이터가 있다고 생각해보자. 가장 먼저 배깅의 특징으로 새로운 학습데이터를 Bootsrap(복원 추출)을 고려하여 n개의 새로운 학습 데이터를 구성한다. 그 후 이 새로운 학습 데이터를 이용하여 d개의 특성 변수 중 임의로 k개의 특성 변수를 뽑아 의사결정나무 즉, Tree를 구성한다. 마지막으로 이를 M번 반복하여 Forest를 구성한다. 여기서 일반적으로 M이 커질 수록 성능이 좋아진다. 즉, Forest안에 Tree들이 많으면 많을 수록 좋다는 뜻이다. (M은 Resource에 맞게 최대로 설정)
3. 부스팅(Boosting)
부스팅은 배깅과 마찬가지로 하나의 분류 알고리즘을 여러번 이용하여 분류를 결정한다. 하지만 부스팅은 학습 시 샘플을 뽑을 때 이전 모델에서 잘못 분류된 데이터를 재학습(혹은 가중치)에 사용하여 순차적으로 처리를 한다. 즉, 배깅과는 학습데이터를 이용하는 방식에 차이를 보인다. 이런 부스팅에는 대표적으로 에이다부스트(Adaboost), 기울기 부스팅(Gradient Boosting, Light Gradient Boosting) 등이 있다. 이들이 어떻게 동작하는지 확인해보자. (추가로 최근에 각광을 받고 있는 CatBoost, XGboost는 다음 파트에서 진행한다.)

1) 에이다 부스트(Adaboost)
(직관적 이해를 위해 분류를 기준으로 설명)
에이다 부스트(Adaboost)는 순차적으로 weak learner를 적용하여 모델을 구성한다. 즉, weak leaner의 조합을 통해 결론적으로 strong learner를 만드는 기법이다. 여기서 weak learner란, 임의로 생성된 분류기보다 약간 더 좋은 모델을 말한다. 이는 이전 분류기에서 잘못 분류된 데이터에 가중치를 적용하여 앞선 모형이 잘 풀지 못했던 Hard cases를 더 잘 풀 수 있도록 학습이 진행된다. 예시를 통해 확인해보자.

범주가 ●와 ▲인 데이터를 분류한다고 하자, 이때 이 데이터에 대해 임의로 생성된 분류기를 통해 일단 분류를 진행한다. 이 결과가 바로 1번이다. 하지만 여기서 ▲와 같은 범주로 잘못 분류된 ●가 2개 보일 것이다. 이게 바로 Hard cases이다. 에이다부스트는 해당 Hard cases를 풀기위해 다음 분류기가 잘못 분류된 ●에 집중해서 분류할 수 있도록 해당 ● 2개에 다른 개체들보다 큰 가중치를 부여하게 된다. 그 결과로 생성되는 2번 분류기가 바로 weak learner이다. 그럼 2번 분류기에선 위의 예시와 같은 결과를 얻을 수 있게 되는 것이다. 하지만 보다시피 2번 분류기에서도 잘못된 분류가 일어난 것이 보일 것이다. 그럼 이제 이 잘못된 ● 3개에 큰 가중치를 부여하여 분류를 시작하게 된다. 결국 이 과정을 순차적으로 진행하면서 지금까지 분류했던 과정들을 통합하여 최종 strong learner를 생성하게 되는 것이다.
이런 에이다부스트는 이론이 쉬운만큼 구현이 쉽고 과적합에 견고하며 배깅방법의 Randomforest보다 속도도 빠르고 정확하다는 장점이 있지만, 잘못 분류된 개체를 수정해가는 알고리즘이기에 노이즈나 이상치에 민감하다는 단점이 있다.
2) 기울기 부스팅(Gradient Boosting)
(직관적 이해를 위해 회귀를 기준으로 설명)
Gradient Boosting은 Gradient Descent와 Boosting의 합성어이다. Gradient Descent는 로지스틱 회귀에서 많이 언급했던 경사하강법이다. 즉, Gradient Boosting은 경사하강법에 Boosting기법을 적용한 것이다. 즉, boosting의 특징은 weak learner를 추가하여 잔차를 예측하도록 하는 방법인 것이다. (잔차가 이용되기에 손실함수가 정의되어야 함. 회귀: MSE..., 분류: Bernoulli loss...) 이때 학습은 순차적으로 앞선 모델이 예측하지 못한 차이를 바로 뒤에오는 추가 모델에서 보상하는 구조로 진행된다. 즉, 이전 모델이 못 맞추고 있는 만큼을 Adaboost에선 그 오차 만큼을 데이터 자체에 가중치를 주어 그 오차를 중점적으로 학습을 하는 것이고 Gradient Boosting은 데이터는 그대로 두고, 우리가 추정해야 되는 그 목표값을 잔차로 둠으로써 이 자체를 학습하는 것이다. (이전에 못맞춘 만큼만 맞추자!) 예시를 통해 살펴보자.

이렇게 데이터가 주어져 있다고 했을 때 가장 먼저 목표값에 대한 예측값을 산출하게 된다. 그 후 그 예측값과 목표값의 차이인 잔차, 즉 해당 모델이 맞추지 못한 정도를 다음 모델이 받아 이에 대한 학습을 진행하는 것이다. 이를 간단히 식을 통해 확인해보면 (물론 훨씬 더 많은 모델들이 필요)


결론적으로 수식을 통해서도 확인할 수 있듯이 잔차를 학습한 모델들이 잘만 학습된다면 최종 목표인 목표값에 근사할 수 있는 것이다. 이렇기에 Gradient Boosting은 잔차를 예측하도록 학습을 진행하는 것이다.
하지만 이런 기울기 부스팅은 과적합에 빠지기 쉽다는 단점이 있다. 아무래도 잔차 그 자체를 모델링하여 학습을 진행하다보니 노이즈까지 모델에 반영이되는 문제가 생기는 것이다. 이런 단점을 줄이기 위해선 Subsampling 혹은 Shrinkage 혹은 Early Stopping이 필요하다.
Subsampling은 이름 그대로 전체 데이터를 사용하지 않고 전체 데이터의 약 80%를 Bootstrap을 허용하며 반복적으로 사용하는 것을 말한다.

여기서 계속해서 80%의 데이터라는 것은 바로 이전의 이미 80%로 설정된 데이터의 80%가 아닌 데이터2에 적용된 f2(x)라는 목표를 데이터1에 적용하여 그 적용된 데이터1의 80%를 다시 샘플링하는 것을 말한다. 이처럼 전체 데이터가 아닌 일부 데이터를 학습에 이용하게 되면 계속해서 똑같은 데이터로 학습하지 않게 되어 노이즈에 견고해지고 일반화 능력이 좋아진다.
Shrinkage는 잔차 모델의 영향력을 조금씩 줄이는 방법을 이야기한다. 즉, 잔차로 인해 생기는 과적합이므로 지속적으로 생기는 잔차, 즉 weak learner의 영향력을 점점 줄이는 것이다.

마지막으로 Early Stopping은 학습 진행에 따른 검증 오차를 통한 과적합 방지법이다. 이는 딥러닝 학습 시에도 사용되는 과적합 방지 기법이다.

학습데이터의 오차를 보면 학습이 진행될 수록 오차가 줄어들지만 검증데이터, 즉 학습에 이용되지 않은 데이터의 오차는 어느 순간부터는 증가하는 것을 볼 수 있다. 즉 해당 시점에서 과적합이 발생하기 시작한 것이다. Early Stopping은 이를 이용하여 학습이 완료되기 전 해당 지점에서 학습을 종료하여 과적합을 방지하는 기법을 사용하는 것이다.
하지만 이런 해결책을 적용함에도 불구하고 Gradient Boosting은 모든 데이터, 모든 특성 변수에 대해서 해당 알고리즘이 수행되기 때문에 비효율적이며 느리다는 단점을 가지고 있다. 이를 더 효율적으로 사용하기 위해 나온 것이 바로 Light Gradient Boosting Machine 즉, LightGBM이다.
3) LightGBM
LightGBM은 GOSS(Gradient-based One-Side Sampling), EFB(Exclusive Feature Bundling) 2가지 방법을 이용하여 기존 GBM 동작 방식을 효율적으로 바꾸었다.
3-1) GOSS(Gradient-based One-Side Sampling)
GOSS는 모든 데이터를 사용하는 GBM의 비효율성을 해결하기 위한 기법이다. 앞선 이론들을 통해서 우린 Gradients가 큰 데이터일 수록 결론적으로 학습 모델에 영향을 크게 미치는 데이터인 것을 알았다. 이 개념을 통해 '그럼 가중치가 큰 데이터들을 중점적으로 포함하자!'가 GOSS의 핵심 개념이다. 즉, 작은 gradients를 가지는 데이터는 랜덤하게 뽑고, 내가 원하는 비율의 큰 gradients를 가지는 데이터는 챙기자는 것이다.

이는 그림과 같이 각 데이터의 Gradient를 오름차순으로 정렬을 한 뒤 내가 선택하는 비율에 따라 Large Gradient를 가진 데이터가 필수적으로 선택되고 나머지 Small Gradient는 랜덤하게 선택되게 된다.
3-2) EFB(Exclusive Feature Bundling)
EFB는 모든 특성 변수를 사용하는 GBM의 비효율성을 해결하기 위한 기법이다. 이는 데이터가 매우 Sparse할 경우(ex: one-hot encoding)에 적용하게 되면 더 좋다. EFB는 이를 서로 거의 독립(서로 영향X)인 특성변수를 묶어서, 하나의 변수로 표현하며 진행한다. 그럼 이때 결국 어떤 데이터를 하나로 묶으며 이 묶은 것을 어떻게 표현할 것이냐가 중요할 것이다. 이는 Greedy Bundling, Merge Exclusive Features를 통해 설명할 수 있다.
Greedy Bundling은 각 2개의 특성 변수의 관계에 집중하여 문제를 풀어나간다. 즉, 각 2개의 특성 변수 둘다 0이 아닌 개수를 표현한 행렬을 통해 정해진 비율에 따라 변수를 묶어주거나 남긴다. 예시를 통해 확인해보자.

예를 들어 10개의 데이터와 5개의 특성변수에 대해 적용된다고 생각해보자. 이때 각 데이터와 특성변수의 값을 표현한 결과를 통해 두 변수 모두 0이 아닌 개수들을 행렬을 통해 표현해 준다. 예를 들어 x1과 x2에 대한 결과를 확인해보면(주황색 형광펜), x1과 x2 둘다 0이 아닌 I(데이터)는 총 6개이다. 이 값을 오른쪽의 행렬에 기록해주는 것이다.
그럼 이제 이 결과를 통해 묶을 변수와 묶지 않을 변수를 비율에 따라 선택하게 된다.


여기서 설정한 cut-off 비율이 0.2라면 즉, cost(=총 데이터 수 x cut-off)가 2(10*0.2)이상인 연결 선들은 자른다고 할 때, 남는 선은 행렬에 형광색을 칠한 3개일 것이다. 이 때 더 적은 특성변수를 선택하기 위해 x1x4, x3x2를 선택하고 x2x4는 잘라준다. 이렇게 되면 총 특성변수는 x1x4, x2x3, x5 이렇게 3개가 남는 것이다. 결국 특성 변수는 Greedy bundling을 통해 5개에서 3개로 줄게 된다. 그렇다면 이 묶인 데이터들에 대해선 어떻게 변경해줘야 될까? 이때 바로 Exclusive feature merging 기법이 사용되는 것이다.
Exclusive feature merging은 묶여진 두 변수 중 한 변수를 기준으로 새로운 변수에 대한 값을 정해주는 기법이다. 이는 바로 예시를 통해 확인해보자.
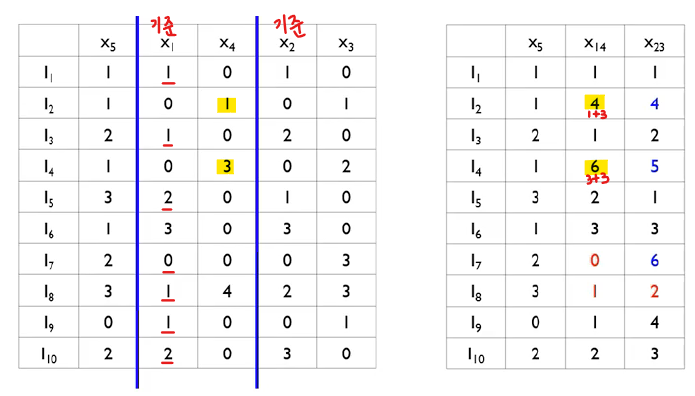
위의 과정을 통해 우린 x1과 x4, x2와 x3가 묶여야 된다는 것을 알아냈다. 그러므로 새로운 x14, x23의 값을 정해야되는데 이때는 결국 더 중요하게 생각 되는 변수를 기준으로 값을 정하면 된다. 이를 x1과 x4가 묶인 새로운 x14가 정해지는 과정을 통해 설명하겠다. 먼저 x1이 x4보다 중요 변수라고 생각이 된다면 x1을 기준으로 둔다. 그 후 x1의 값이 0인 동시에 x4가 값이 존재하는 경우는 x4의 해당 값과 x1의 최대값(3)을 더해준 값으로 새로운 값을 정해준다. 이 외에는 모두 x1의 값을 그대로 사용하게 된다. 이런 과정을 통해 결국 x14, x23이 정해지며 특성 변수를 줄일 수 있게 되는 것이다.
실습
이번 실습은 실제 은행에서 대출을 하냐 안하냐를 따지는 데이터인 UniversalBank를 통해 진행한다.
import pandas as pd
import numpy as np
bank_df = pd.read_csv('UniversalBank.csv') # 카드 개설 관련 데이터
bank_df.head(3)
이제 여기서 내가 사용할 특성변수와 사용하지 않을 특성변수를 선택하여 데이터를 새로 만들어 준다. (이 때 사용되는 것이 도메인 지식 혹은 독립변수들의 상관관계를 EDA를 통해서 분석. - 하지만 모델 예측에 집중하기 위해 생략함)
x = bank_df.drop(['ID','ZIPCode','PersonalLoan'], axis=1)
#ID와 ZIPcode는 고유번호 이기에 없애줌, PersonalLoan은 맞추어야 할 목표값Y.
y = bank_df['PersonalLoan']
1. 다수결 투표(Majority Voting)
이제 Majority Voting에 사용될 학습 모델들을 설정해준다. 다수결 투표는 앞서 말했듯이 여러 분류기의 결과를 투표를 통해 가장 많이 나온 결과를 새로운 데이터에 할당한다.
#Majority Voiting의 앙상블 학습에 사용되는 모델 개별 정의
from sklearn.tree import DecisionTreeClassifier # 의사결정나무
from sklearn.neighbors import KNeighborsClassifier # KNN
from sklearn.linear_model import LogisticRegression # 로지스틱 회귀
logistic = LogisticRegression(solver='liblinear', penalty='l2', C=0.001, random_state=1)
# solver는 liblinear 알고리즘 선택, l2 규제화, C 규제강도는 0.001 선택
knn = KNeighborsClassifier(n_neighbors=5, p=2)
# 참고할 이웃은 5개, 거리측정은 유클라디언 거리 측정 사용
tree = DecisionTreeClassifier(max_depth=None, criterion='entropy', random_state=1)
# 엔트로피 불순도 측정법 사용. 즉, C4.5 알고리즘 사용, 최대 깊이는 설정하지 않고 default값으로모델은 의사결정나무, KNN, 로지스틱 회귀를 사용했으며, 각각의 하이퍼파라미터는 추후에 조정할 것이기에 임시로 설정해 두었다. (각각의 하이퍼 파라미터에 대해 자세히 알고싶다면 이전 파트 확인 바람)
이제 다수결 투표기법을 사용하여 앙상블을 적용해보자. (Majority Voting은 sklearn에서 제공)
#해당 모델들을 이용하는 Majority Voting 정의
from sklearn.ensemble import VotingClassifier # Mjority Voting에 사용되는 메서드
voting_estimators = [('logistic',logistic),('tree',tree),('knn',knn)] # 내가 사용할 모델들에 대해 이름 정의
voting = VotingClassifier(estimators=voting_estimators, voting='soft') # Mjority Voting
# 사용되는 학습 모델들은 이전에 설정했던 학습 모델들여기서 VotingClassifier에 사용되는 voting인자는 hard와 soft로 나뉘어 진다. hard는 위에서 설명한 투표를 통한 결정을 말하고 soft는 확률을 통한 결정을 말한다. 즉, soft는 3가지 모델의 해당 클래스에 대한 확률의 평균이 더 큰 클래스로 개체의 새로운 범주를 결정한다.
이제 각각의 모델의 예측결과와 다수결 투표를 통한 예측결과를 교차검증을 통해 확인해보자
# voting을 쓰는 것이 옳은지 판단. (교차검증이용) -> 각각에 대하여 성능확인
from sklearn.model_selection import cross_val_score
clf_labels = ['DecisionTreeClassifier','KNeighborsClassifier', 'LogisticRegression', 'Majority voting']
all_clf = [tree, knn, logistic, voting] # 각 학습 모델, 마지막은 다수결투표 모델
for clf, label in zip(all_clf, clf_labels):
scores = cross_val_score(estimator=clf, X=x, y=y, cv=10, scoring='roc_auc')
print('[%s] ROC_AUC : %.4f (+/-%.4f)' %(label, scores.mean(), scores.std()))
역시 Majority Voting의 결과가 젤 좋다. 그럼 이제 이 Majority Voting의 각 학습 모델의 하이퍼파라미터를 GridSearchCV를 통해 조정해 보자. (GridSearchCV는 모델의 하이퍼파라미터가 가질 수 있는 경우의 수를 확인하여 최적의 결과를 얻는 모델을 교차 검증을 통해 결정해줌. 파트9 참고)
#voting이 best모델이므로 GridSearchCV를 통한 최적의 모델 및 파라미터 확인
from sklearn.model_selection import GridSearchCV
params = {'logistic__C':[0.001,0.1,100.0], #개별 모델에 대한 파라미터 설정
'tree__max_depth':[1,3,5],
'knn__n_neighbors':[1,3,5]}
gs_cv = GridSearchCV(estimator = voting, param_grid=params, cv=10, scoring='roc_auc') # 설정
# 설정된 파라미터들의 모든 경우의 수를 통해 가장 좋은 성능을 낸 모델을 교차검증을 통해 산출함
gs_cv.fit(x, y) # 실행
print(gs_cv. best_params_) #결과의 최적의 파라미터
print(gs_cv.best_score_) #결과의 최적의 성능 점수
이전의 결과보다 더 좋은 결과를 얻게 되었다. 만약 리소스가 충분하다면 더 다양한 인자와 경우의 수를 확인할 수 있다.
2. 배깅(Bagging)
배깅은 앞선 이론에서 봤듯이 하나의 분류기(DecisionTree)를 여러번 사용하여 분류를 진행한다.
먼저, 하나의 분류기에 해당하는 의사결정나무를 생성해준다. (바로 RandomForest로도 Bagging 가능)
#bagging에 사용될 Classifier 선언 - DecsionTree
from sklearn.tree import DecisionTreeClassifier # 의사결정나무 for 분류
tree = DecisionTreeClassifier(max_depth=None, criterion='entropy',random_state=1)
# 최대 깊이는 설정해주지 않고, C4.5(엔트로피) 알고리즘 사용그 후 이를 여러번 사용할 Bagging 앙상블 모델을 만들어준다.
#해당 모델을 이용하는 Bagging 정의 (tree를 반복적으로 사용하는 것임)
from sklearn.ensemble import BaggingClassifier
bagging = BaggingClassifier(base_estimator=tree, n_estimators=100,
bootstrap=True, bootstrap_features= False,n_jobs=1, random_state=1)
# 100개의 개별 모델을 통해 여러번 진행하고 데이터 사용 시 중복 추출 사용.방금 설정한 DecisionTree를 배깅을 통해 100개를 생성하여 Forest(RandomForest)를 만들어보자.
그 후 기존의 하나만 사용된 Decision Tree와 Bagging의 모델의 결과를 비교해보자.
#ensemble을 사용할지 기존모델인 DecsionTree를 사용할지 비교 (평가)
from sklearn.model_selection import cross_val_score # 교차검증
clv_label = ['DecisionTree','Bagging']
all_clv = [tree, bagging]
for clv, label in zip(all_clv, clv_label):
score = cross_val_score(estimator=clv, X=x, y=y, scoring='roc_auc',cv=10) #10개의 검증샘플
print('[%s] ROC_AUC: %.4f' %(label, score.mean()))
당연히 Tree를 앙상블로 만들어 사용하는 Bagging의 결과가 확연히 좋은 것을 확인할 수 있다.
이제 앞서 진행했던 GridSearchCV를 통해 최적의 하이퍼 파라미터를 결정해 준다.
#Bagging이 더 성능이 좋기 때문에 Bagging에서 Tree의 파리마터를 자동으로 선택
from sklearn.model_selection import GridSearchCV
params = { 'base_estimator__max_depth':[None,1,3,5], 'base_estimator__criterion':['entropy', 'gini']}
#bagging.get_params().keys()를 통해서 사용해야할 이름 (base_estimator__criterion,,,이런거 확인)
grid = GridSearchCV(estimator=bagging, param_grid=params,cv=10, scoring='roc_auc')
grid.fit(x, y)
print(grid.best_params_) # 최적의 하이퍼파라미터
print(grid.best_score_) # 최적의 결과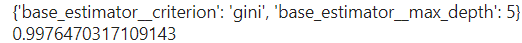
3. AdaBoost
에이다 부스트는 앞서 설명했다시피 boosting 기법을 통해 학습 및 분류를 진행한다. 고로 먼저 의사결정나무를 생성해준다.
#boost에 사용될 모델 정의 (Tree)
from sklearn.tree import DecisionTreeClassifier # 의사결정나무
tree = DecisionTreeClassifier(max_depth=1, criterion='entropy',random_state=1)이제 사용할 AdaBoost를 선언하고 설정해준다.
# Boosting 기법의 ADABoost 사용
from sklearn.ensemble import AdaBoostClassifier
adaboost = AdaBoostClassifier(base_estimator=tree, n_estimators=100,
learning_rate = 0.1, random_state=1)이때 중요한 것은 AdaBoost의 하이퍼 파라미터들이다. n_estimators를 100으로 두면서 100개의 의사결정나무를 사용하여 boosting 기법으로써 잘못 분류된 데이터에 가중치를 주며 반복적으로 weak learner 학습해 나가며 결론적으로 strong learner를 생성한다. 이때 학습에 가중치가 사용되기에 learning rate가 하이퍼파라미터로 설정되어 있는 것을 확인할 수 있다.
이제 GirdSearchCV를 통해 최적의 하이퍼파라미터를 설정해보자.
#파리미터 자동 설정으로 성능 올리기
from sklearn.model_selection import GridSearchCV
params = {'base_estimator__criterion':['entropy', 'gini'], 'base_estimator__max_depth':[None,1,3,5]}
grid = GridSearchCV(estimator=adaboost, param_grid=params, scoring='roc_auc', cv=10)
grid.fit(x,y)
print(grid.best_params_)
print(grid.best_score_)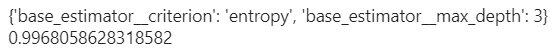
좋은 결과를 확인할 수 있다.
4. GBM, LGBM
이제 마지막으로 Gradient Boosting Machine과 이의 개선 버전인 Light GBM을 사용해보자.
GBM이나 LGBM은 둘 다 기본 학습 모델을 DecisionTree로 설정해두기에 따로 선언해줄 필요는 없다.
#Tree가 기본 모델로 설정되어 있음
from sklearn.ensemble import GradientBoostingClassifier
gbm = GradientBoostingClassifier(n_estimators=100, learning_rate=0.5,random_state=1)여기서 중요한 것은 learning_rate이다. GBM은 이름에서 알 수 있듯이 Gradient를 사용하고 잔차를 학습하기에 손실함수가 정의 되어 경사하강법이 사용된다. 경사하강법에서의 중요한 부분은 학습률이라고 로지스틱함수에서 언급했던 것을 기억해보자. 그에 따라 결국 GBM에서도 learning_rate은 중요한 하이퍼파라미터가 된다.
이제 이런 인자들을 자동으로 조합하여 성능을 올려보자.
#파리미터 자동 설정으로 성능 올리기
from sklearn.model_selection import GridSearchCV
params = {'learning_rate':[0.8,0.5,0.3], 'max_depth':[None,1,3,5]}
grid = GridSearchCV(estimator=gbm, param_grid=params, scoring='roc_auc', cv=10)
grid.fit(x,y)
print(grid.best_params_)
print(grid.best_score_)
앞선 모델들과는 달리 GBM에선 learning_rate이 중요하기에 learning_rate까지 조절해보았다.
이제 GBM의 개선 버전인 LGBM을 간단히 사용해보자.
LGBM도 GBM처럼 따로 DecisionTree를 설정하지 않아도 기본 모델을 Decision Tree로 사용한다.
from lightgbm import LGBMClassifier
lgbm = LGBMClassifier(n_estimator=100, learning_rate=0.5, random_state=1)
lgbm.fit(x,y)#파리미터 자동 설정으로 성능 올리기
from sklearn.model_selection import GridSearchCV
params = {'learning_rate':[0.8,0.5,0.3], 'max_depth':[None,1,3,5]}
grid = GridSearchCV(estimator=lgbm, param_grid=params, scoring='roc_auc', cv=10)
grid.fit(x,y)
print(grid.best_params_)
print(grid.best_score_)
똑같은 설정으로 진행을 해도 LGBM이 GBM보다 성능이 좋고 가동시간이 훨씬 빨랐다. 이런 이유에서 실제로도 GBM보다는 그의 개선버전인 LGBM을 더 많이 사용한다.
이번 파트는 이렇게 앙상블에 대하여 이론을 알아보고 실습을 진행해보았다. 다음 파트는 최근 머신러닝에서 각광받고 여러 곳에서 자주 사용되는 GBM의 개선버전에 대해 알아보고 머신러닝 전체 과정를 마무리하려 한다.