2021년도에 대학교 과목으로 들었던 '기계학습' 강의를 복습 및 정리 + 추가적인 공부를 위해 이 글을 작성한다. (세종대학교 최유경 교수님 '2021 기계학습'수업)
저번 파트까진 지도학습(Supervised learning)에 대해 배우고 지도학습의 대표적인 학습 모델에 대해서 알아보았다.이번 주차부터는 지도학습과는 다른 비지도학습(Unsupervised learning)에 대해 알아보고 비지도학습의 대표적인 학습 모델을 소개하려 한다.
비지도학습(Unsupervised Learning)
비지도학습은 말 그대로 학습을 지도하는 가이드 라인(결과값)이 없다고 생각하면 된다. 즉, 입력값에 대한 결과값(목표값)이 주어지지 않은 상태에서 데이터가 어떻게 구성되었는지를 중점적으로 학습을 진행한다. 지도학습과는 가이드 라인(결과값)이 있냐 없냐의 차이를 보인다. 이는 크게 군집화(clustering), 변환(transform), 연관(association)으로 나누어진다.
군집화는 비슷한 것을 찾아서 그룹을 만드는 것이다. 군집화의 대표적인 방법에는 분리형 군집화(K-means), 분포 기반 군집화(DBSCAN)이 있다. 얼핏보면 군집화가 분류와 차이가 없다고 생각할 수 있지만, 둘은 다른 개념이다. 이에 대해서 밑에서 더 자세히 다룰 예정이다. 변환은 데이터를 새롭게 표현하여 사람이나 학습 모델이 원래 데이터보다 쉽게 해석할 수 있도록 만드는 것이다. 대표적으로 비지도학습 기반 차원 축소인 주성분 분석(PCA)이 있다. (이전에 다루었던 DA에서 사용되는 차원축소는 지도학습 기반 차원축소) 연관은 서로 연관된 특징(열)을 찾아내는 것이다. 이는 주로 추천과 관련된 부분에서 사용된다.
다양한 비지도학습 중 이번 주차에는 군집화에 대해 자세히 다루어 보려한다.
군집화
이론
군집화는 다시 얘기하자면 유사한 속성을 갖는 데이터를 묶어 전체 데이터를 몇개의 군집으로 나누는 것이다. 즉, 데이터의 클래스(목표값)가 주어져 있지 않은 상태에서 데이터의 분포 및 특성들만을 참고하여 몇개의 군집으로 나눈다. 예시를 통해 살펴보자.

가장 먼저 클래스(목표값, 범주)가 주어져 있지 않은 데이터들이 있다고 했을 때 (위의 색칠된 것은 군집화의 결과임, 참고용. 원래는 색이 구분되어 있지 않음), 이들의 분포만을 참고하여 오른쪽 결과처럼 그룹을 부여한다. (정해진 클래스가 아닌 임시 클래스(군집1, 군집2, 군집3, ...)할당. 즉, 군집만 한다는 뜻)
그렇다면 좋은 군집화의 기준은 무엇일까? 이는 동일한 군집, 서로 다른 군집에 따른 두가지 기준이 있다. 먼저, 동일한 군집에 소속된 데이터는 서로 유사할 수록 좋은 군집화라고 평가 받는다. 즉, 군집이 완료되었을 때, 각각의 군집들 속의 데이터들이 비슷해야 좋은 군집화라고 판단하는 것이다. 다음으로는 상이한 군집에 소속된 데이터는 서로 다를 수록 좋은 군집화라고 평가받는다. 즉, 서로 다른 군집은 비슷하면 안된다는 뜻이다.

지금까지의 설명을 들으면 사실 군집화와 분류의 차이에 대해 의심할 수 있다. 그럼 도대체 군집화랑 분류는 어떤 차이가 있는걸까?
분류는 애초에 주어진 클래스(목표값, 범주)를 나누는 것이다. 즉, 사전 정의된 범주가 있는 데이터로부터 예측 모델을 학습하는 문제이다. 반면에, 군집화는 주어진 클래스없이 비슷한 개체들끼리 묶어 나가는 것이다. 즉, 사전 정의된 범주가 없는 데이터로부터 최적의 그룹을 찾아가는 문제이다. 간단하게 말하자면 군집화는 그룹을 찾아내기 전까지 확정된 범주가 없고 최적의 그룹을 찾아내야 해당 데이터의 범주(임시 그룹. 군집1, 군집2, ...)가 생기는 것이다.

이런 군집화는 스포츠, 경제, 기술 등으로 군집하기 위해 문서 내 단어를 이용하여 유사 문서를 군집화하는 문서 군집화, 사람, 자동차, 오토바이 등 영상 내의 특징을 이용하여 유사한 영상끼리 군집화하는 영상 군집화, 고객정보와 카드 결제내역을 통해 고객을 그룹으로 군집화하는 고객 군집화 등 생각보다 다양한 분야에서 사용된다.
이제 이 군집화가 어떤 과정을 통해 최적의 그룹을 찾아가는지 알아보자.
군집화는 최적의 그룹을 찾아가는 과정에서 1) 유사도를 어떤 거리측도를 사용하여 측정할 것인지, 2) 어떤 군집화 알고리즘을 사용하며 그 때의 최적의 군집의 수를 어떻게 결정할 것인지, 각각의 알고리즘에 따른 군집화 결과를 어떻게 측정하고 평가할 것인지에 따라 결과가 다양하게 달라진다. 그렇다면 각각의 요소들은 어떻게 정해져야 할지 개념을 살펴보며 확인하자.
1. 유사도 척도
군집화에서의 유사도 척도는 어떤 거리 측도를 사용하여 유사도(similarity metirc)를 측정할 것인지에 대한 선택 과정이다. 여기서 사용되는 거리 측도는 지도학습의 KNN에서 봤던 유클리디언 거리(Euclidean Distance)와 맨하탄 거리(Manhattan Distance), 마할노비스 거리(Mahalanobis Distance)를 사용한다.
1) 유클리디언 거리(Euclidean Distance)
유클리디언 거리는 일반적으로 사용되는 거리 척도이다. 보통 L2 거리로 불리기도 한다. 이는 두 관측치 사이의 직선 거리를 의미하는 간단한 거리 척도를 가지고 있다.
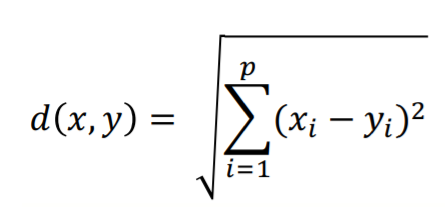
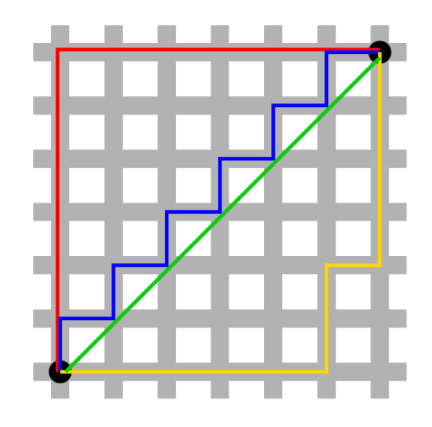
2) 맨하탄 거리(Manhattan Distance)
맨하탄 거리는 직교 좌표계에서 일정한 좌표축의 점 위에 투영한 선분 길이의 합을 말한다. 이는 택시거리 혹은 L1거리라고 불리기도 한다.

3) 마할노비스 거리(Mahalanobis Distance)
마할노비스 거리는 변수 내 분산, 변수 내 공분산을 모두 반영하여 두 지점(X,Y) 간 거리를 계산하는 방식이다. 만약 데이터의 공분산 구조가 Identity구조(원 구조)인 경우는 유클리디언 거리 척도로 측정된다.


이렇게 군집화는 개체간의 유사도를 측정할 때 위의 3가지의 거리를 사용하여 측정이 가능하다. (이 또한 최적의 거리는 없으며 실험적으로 접근해야 됨, 즉 데이터마다 다름)
이제 군집화에서 사용되는 알고리즘들은 어떤 것들이 있는지, 그 알고리즘들은 최적의 군집을 어떻게 설정하고 어떤 평가지표를 통해 군집화 결과를 평가하는지 알아보자.
2. 군집화 알고리즘
군집화 알고리즘에는 계층적 군집화, 분리형 군집화, 분포 기반 군집화 3가지로 이루어져있다.
1) 계층적 군집화
계층적 군집화는 말 그대로 계층적 트리 모델을 이용하여 개별 개체들을 순차적/계층적으로 유사한 개체 및 군집과 통합시키는 방법을 말한다. 이는 덴드로그램(Dendrogram, 개체들이 결합되는 순서를 나타내는 트리 형태의 구조)를 통해 시각화가 가능하다는 장점이 있다. 또한, 덴드로그램을 생성한 후 적절한 수준에서 자르면 그에 해당하는 군집화 결과가 생성되기에 사전에 군집의 수를 정하지 않아도 된다는 장점도 있다.

이제 계층적 군집화가 어떤 과정을 통해 군집을 이루는지 간단한 예시를 통해 확인해보자.
예를 들어 A,B,C,D 라는 4개의 객체를 대상으로 군집화를 진행하려 한다고 하자. 우린 이 모든 데이터 사이의 거리에 대한 유사도를 계산해야 될 것이다. (앞서 설명한 유사도 척도를 통해 계산)

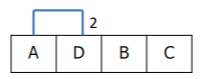
이렇게 유사도 행렬 계산이 마무리 되었다면 이제 거리가 인접한 데이터끼리 군집을 형성하게 된다. 위의 유사도 행렬에서 가장 인접한 데이터(작은 값)는 A와 D이다. 이렇게 가장 인접한 데이터들끼리 군집을 시작하게 된다. A와 D가 묶이게 되면 A와D는 하나의 개체로 보고 이제 이 새로운 개체에 대한 각 개체들의 새로운 유사도를 측정하게 된다.

그리고 앞서 진행했던 것과 같이 이 유사도 행렬을 통해 다시 가장 인접한 개체들(AD, C)끼리 군집화를 진행한다.
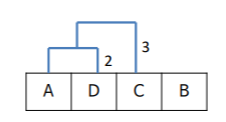
이런 과정을 모든 개체가 군집을 가지게 될 때까지 계속해서 반복한다. 그렇게 되면 해당 예시의 군집화 결과는
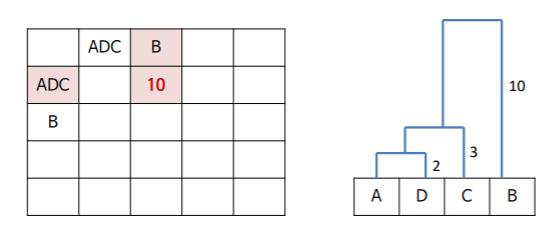
이렇게 될 것이다.
그렇다면 이제 군집의 개수만을 정하면 될 것이다. 앞서 말했듯이 계층적 군집화는 사전에 군집의 개수를 설정하지 않고 군집의 결과인 덴드로그램에서 정할 수 있다 했다. 그럼 해당 예시에선 어떻게 설정하면 될까?
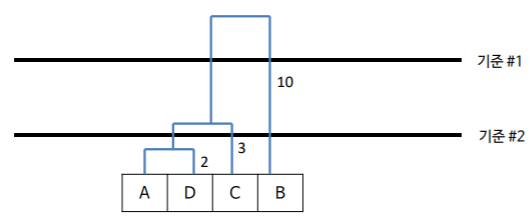
기준1과 기준2 둘 중 하나로 계층을 자르면 된다. 기준1로 자르게 되면 ADC그룹, B그룹 이렇게 2개의 군집이 생길 것이고 기준2로 자르게 되면 AD그룹, C그룹, B그룹 이렇게 3개의 군집이 생길 것이다. 이처럼 계층적 군집화는 군집의 결과를 통해 군집의 개수를 설정할 수 있다.
결국 맨처음에 첨부했던 예시의 데이터는 위 과정을 거쳐 진행되는 것이다.
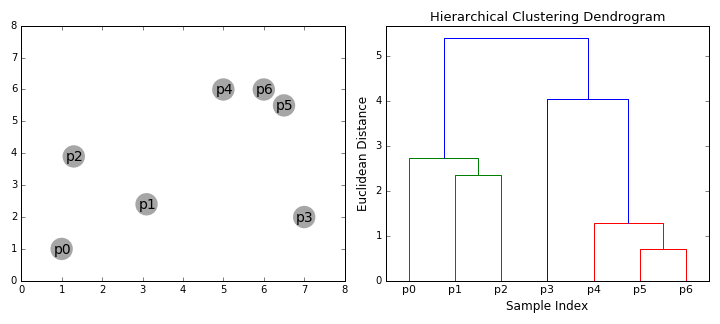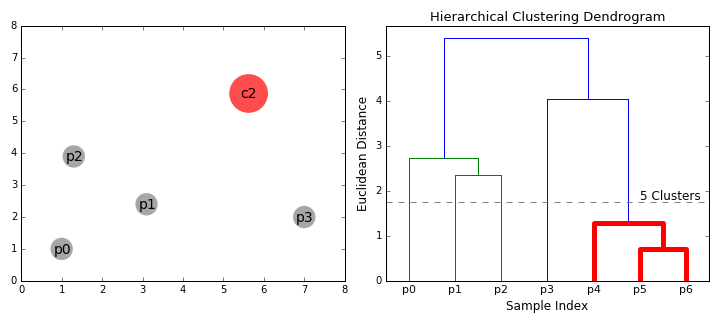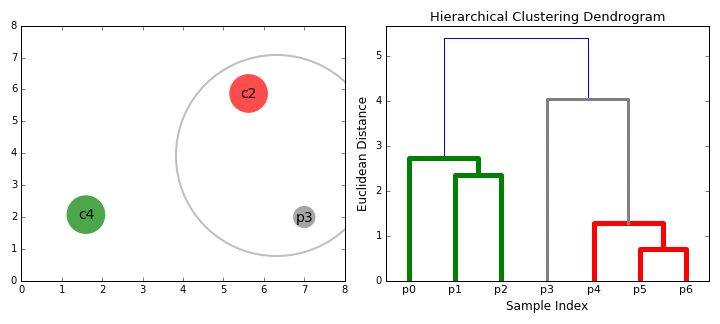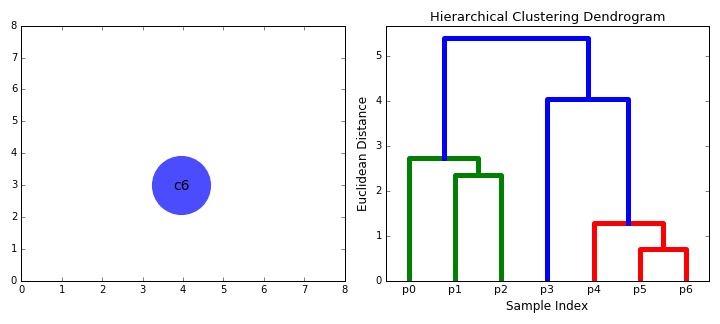
우린 군집 내의 개체의 거리가 최소화되고 군집 간의 거리가 최대화되는 군집화가 좋은 군집화라는 것을 알고 있다. 지금는 군집 내의 개체의 거리(유클리디언, 맨하턴, 마할노비스 등을 통해 계산)가 최소화되게 하며 군집화를 진행한 것을 설명했다. 그렇다면 군집 간의 거리가 최대화되기 위해 사용되는 군집간의 거리 계산 법에는 무엇이 있을까?
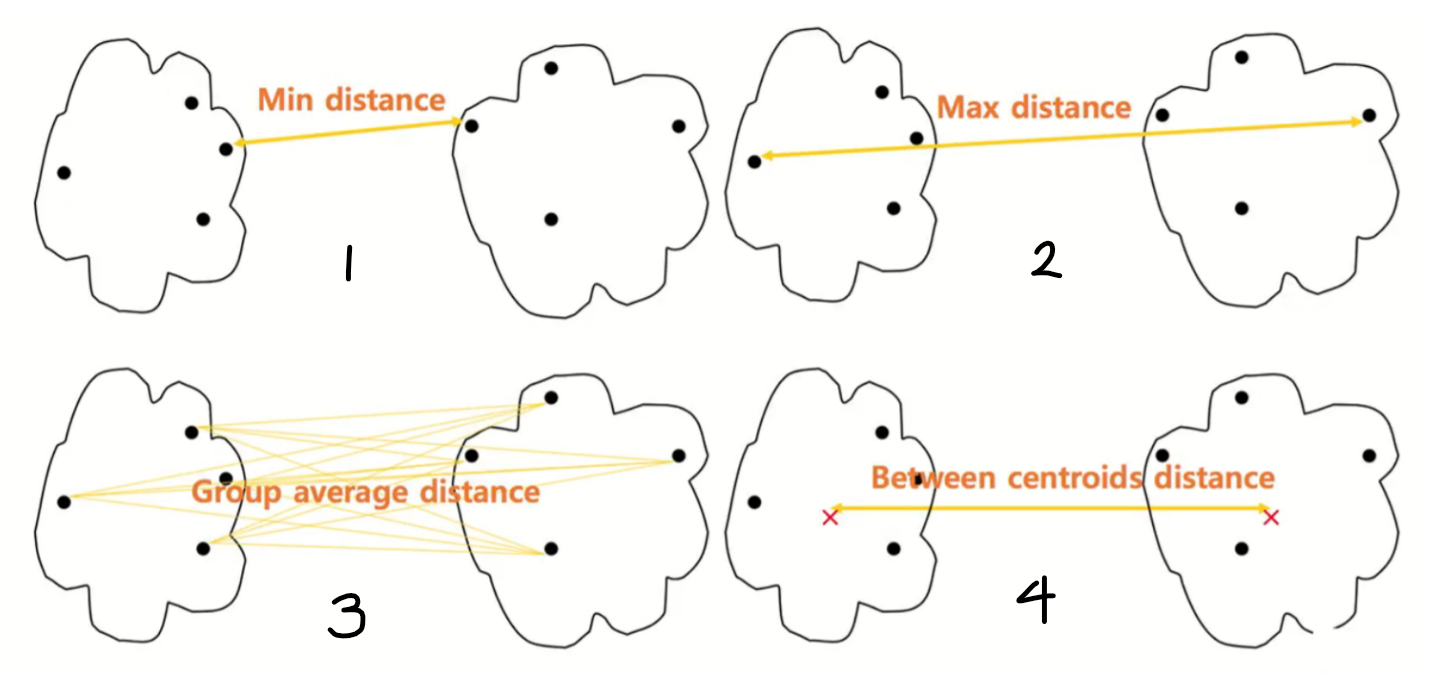
먼저 대표적으로 군집 내 데이터 간 거리를 모두 계산하여 (1)가장 작거나 (2)가장 크거나 (3)평균 거리값을 두 군집의 거리로 측정하는 경우가 있다. 다음으로는 (4)각 군집 내 데이터의 평균을 계산하여 평균과 평균 사이의 거리 값을 두 군집간의 거리로 선택하는 경우가 있다.
마지막으론 Ward거리 계산법(ward linkage method)이 있다. 이는 (1)서로 다른 군집에 해당하는 모든 데이터를 포함한 중심을 구하고, 구한 중심과 서로 다른 군집에 포함되는 모든 데이터 사이의 거리를 구한다. 그 후 (2)각 군집에 해당하는 데이터를 통해 중심을 구한 후 그 중심과 군집 내 데이터 사이의 거리를 구하여 각 군집에 대한 해당 결과를 모두 합해준다. 마지막으로 구한 이 2개의 값(1과 2)를 빼줌으로써 계산된다. 아래의 예시와 같이 Ward 거리 계산법의 결과가 클 수록 서로 다른 군집은 유사도가 낮아 멀리있다는 것이 되고, 작을 수록 서로 다른 군집의 유사도는 높아 가까이 있다는 뜻이 된다.


2) 분리형 군집화 (K-means Clustering)
분리형 군집화에는 군집화에서 유명한 K-means Clustering(K 평균 군집화)이 해당된다.
K-means Clustering의 각 군집은 하나의 중심을 가지게 된다. 각 객체는 그 중심들 중 가장 가까운 중심에 할당되며 결국 그 같은 중심에 할당된 개체들이 모여 하나의 군집을 형성하게 된다. 이는 계층형 군집화와 다르게 사전에 군집의 수 K가 정해져야 수행될 수 있다.
그럼 이 K-means Clustering은 어떻게 동작될까? 예시(K=3)를 통해 알아보자.
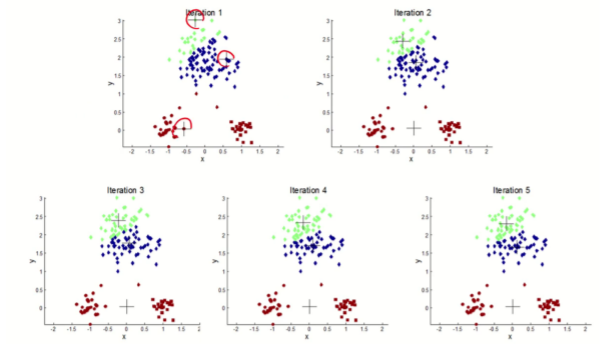
가장 먼저 K개의 중심을 임의로 생성하면서 동작한다. 그 후 생성된 중심을 기준으로 모든 데이터에 가장 가까운 중심에 맞는 군집을 할당하게 된다.

이제 새로 할당된 각 군집의 중심을 다시 계산하게 되고 또 그 중심을 기준으로 모든 데이터에 군집을 다시 새로 할당해준다.

이 과정들을 중심이 변하지 않을 때까지 반복하여 진행하게 된다.

하지만, 맨 처음 시작할 때의 초기 중심 설정(랜덤하게)은 최종 군집화 결과에 영향을 미칠 수 있다. (극히 적은 확률로 발생함)
만약 앞선 예시에서 초기 중심 설정이 우연히 이상하게 설정되었다면 위의 결과와는 다른 이상한 군집화 결과를 확인할 수 있을 것이다.
이런 K-means Clustering의 한계는 다양한 방법으로 극복할 수 있다. 먼저, 여러 번 Kmeans 군집화를 수행하여 가장 여러 번 나타나는 군집을 사용할 수 있다. 이는 앙상블의 개념을 따온 것으로 초기 중심의 한계를 간접적으로 해결한 케이스이다. 다음으로는 데이터 분포 정보를 활용하여 초기 중심을 선정하는 방법이다. 이는 데이터가 Gaussian 분포일 경우에 가능하며, 가우시안의 평균(중심)을 초기 값으로 선정하여 직접적으로 해결한 방법이다. 마지막으로는 데이터의 일부를 활용(샘플링)하여 계층적 군집화를 수행한 뒤 그 결과를 이용하여 초기 군집 중심으로 사용하는 방법도 있다. 이 또한 직접적으로 한계를 극복한 경우이다.
하지만 한계는 이뿐만이 아니었다. K-means Clustering은 (1) 서로 다른 크기의 군집을 잘 찾아내지 못하며, (2) 서로 다른 밀도의 군집 또한 잘 찾아내지 못한다. 또한, (3) 지역적 패턴이 존재하는 군집을 판별하기에 부족한 모습을 보인다.
이게 바로 분포 기반 군집화(DBSCAN)가 나오게 된 배경이기도 하다.



지금까지는 분리형 군집화가 이루어지는 과정에 대해 알아보았는데, 그럼 계층형 군집화와 달리 시작하기 전 K를 설정하는 분리형 군집화(K-means Clustering)은 어떻게 K를 선정할까?
분리형 군집화는 다양한 군집 수에 대한 성능 평가 지표를 통해 최적의 군집 수(K)를 선택한다. 이는 일반적으로 성능지표와 군집수의 관계를 표현한 그래프를 통해 Elbow point(그래프가 꺽이는 지점)가 보이는 지점을 최적의 군집 수로 선정한다.

여기서 사용되는 성능 지표(군집화 평가 방법)는 SSE(Sum of Squared Error)이다. 하지만 이 SSE는 군집 내 거리의 최소화는 평가가 가능하지만 군집 간 거리가 최대화가 되었는지는 판단이 불가능하다는 단점을 가지고 있다. 결국 SSE를 통해서 해당 군집의 결과가 좋은 군집의 결과인지 확실하게 알 수 없다는 뜻이다. 그래서 사용하게 된 성능 지표가 바로 silhouette 통계량이다.
silhouette 통계량은 먼저 (1) 해당 데이터(i번째 데이터)와 같은 군집 내에 있는 모든 데이터 사이의 평균 거리를 구하고 (2) 해당 데이터(i번째 데이터)와 다른 군집 내에 있는 모든 데이터 사이의 최소 거리를 구한 결과를 조합하여 평가 지표로 사용하게 된다. [(1)은 a(i)에 해당, 작을 수록 유사한 데이터가 한 군집에 모여있다는 뜻 | (2)는 b(i)에 해당, 클수록 각 군집이 잘 흩어져 있다는 뜻]


일반적으로 이 s(i)값이 0.5보다 크면 군집 결과가 타당하다고 판단하고 1에 가깝다면 좋은 군집화, -1에 가깝다면 나쁜 군집화라고 판단한다. (여기서 보통 k=2인 경우 Best값으로 나오는 문제가 있기에 차 순위 K를 선정하는 것이 일반적임)
3) 분포 기반 군집화
분포 기반 군집화는 앞서 설명한 분리형 군집화의 한계를 해결할 수 있는 방법이다. 이는 대표적으로 DBSCAN(Density Based Clustering)이 있다. DBSCAN은 높은 밀도를 가지고 모여 있는 데이터들을 그룹으로 선정하고 낮은 밀도를 가지고 있는 데이터는 이상치 혹은 잡음으로 선정하는 것을 기본으로 두고 군집화를 진행한다. 이는 기준인 데이터의 e 거리 안에 M개 이상의 데이터를 포함하는지의 여부에 따라 그룹이 될지 이상치/잡음이 될지 판단한다. 즉, e와 M은 DBSCAN의 설정되어야할 하이퍼 파라미터인것이다. (e: 너무 작으면 많은 데이터가 잡으로 분류, 너무 크면 군집의 개수가 작아짐 / M: 일반적으로 "특성 변수의 개수 +1"을 사용)
DBSCAN은 개체를 핵심자료, 주변자료, 잡음자료 3가지로 분류해서 판단하며 군집화를 진행한다. 핵심자료(core point)는 e-neighborhood(e거리 안에 있는 이웃의 수)가 M개 이상의 데이터를 포함하는 자료를 말한다. 말 그대로 핵심자료로 그룹을 결정하는 데 큰 중요도를 가지고 있는 자료이다. 주변자료(border point)는 핵심자료는 아니지만 e-neighborhood에 핵심자료를 포함하는 자료를 말한다. 마지막으로 잡음자료(noise point)는 핵심자료도 주변자료도 아닌 자료를 말한다.
그렇다면 이런 DBSCAN은 어떤 과정으로 군집화를 진행할까? DBSCAN은 먼저 임의의 데이터를 선택하고 이를 그룹 1로 설정한다. 그 후 그 데이터의 e-neighborhod를 구하고 그 데이터의 수가 M보다 작으면 이 데이터를 잡음자료로 부여하고 M보다 크다면 그 데이터를 포함한 모든 e-neighborhood에 군집 1을 부여한다. 그리고 군집 1 모든 데이터의 e-neighborhood의 크기가 M보다 큰 것이 없을 때까지 반복한다. 이제 이 모든 과정을 다른 군집에 대해서도 계속해서 동일하게 반복한다. 즉, DBSCAN은 모든 데이터에 군집이 할당되거나 잡음으로 분류될 때까지 위의 과정을 반복해서 진행하는 것이다. 결론적으로 DBSCAN은 바이러스가 퍼지는 과정과 유사하다고 말할 수 있다. 이는 밑의 예시를 보면 알 수 있다.
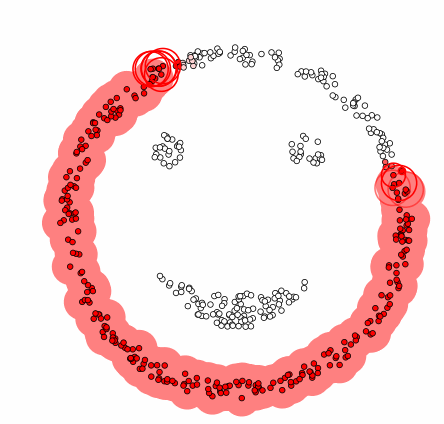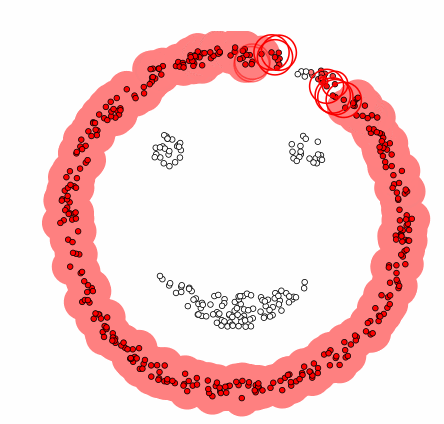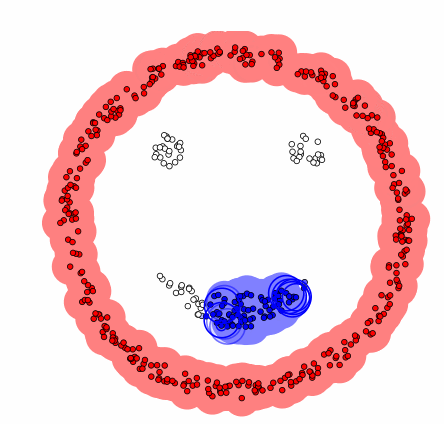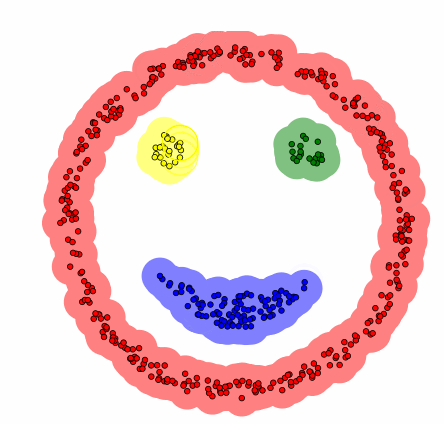
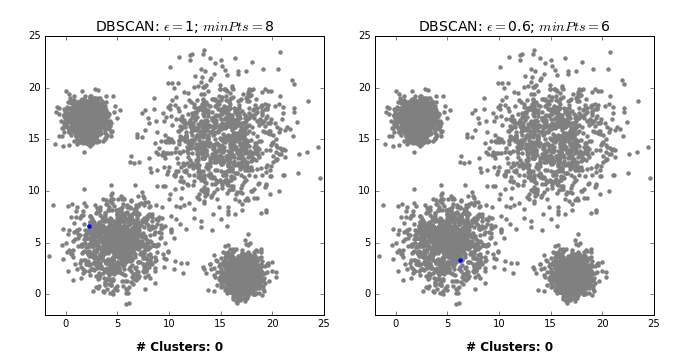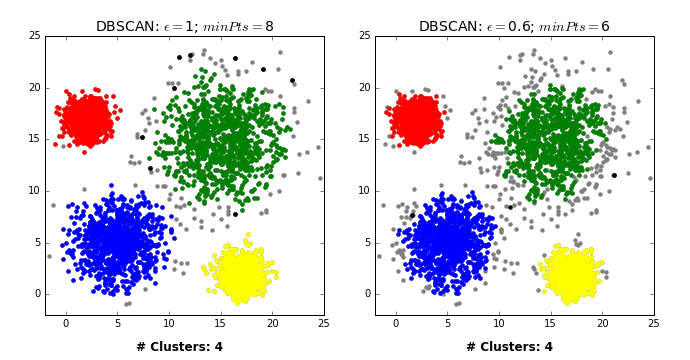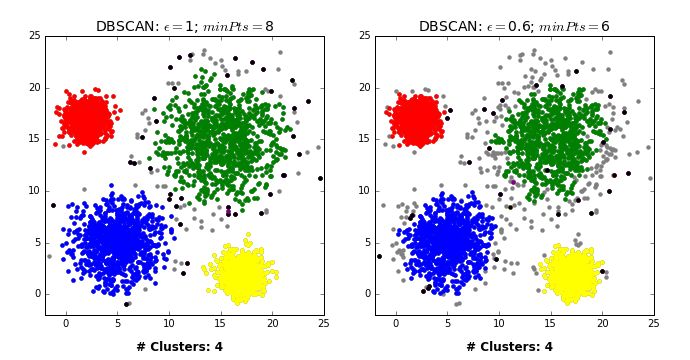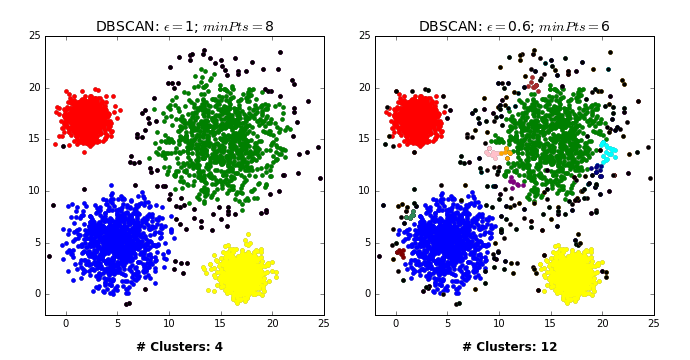
[GIF 출처: https://dashee87.github.io/data%20science/general/Clustering-with-Scikit-with-GIFs/]
실습
1) 계층적 군집화
계층적 군집화는 이전에 사용했던 iris데이터를 사용한다. 하지만 우린 분류가 아닌 군집화를 하는 것이기에 특별히 추가적인 전처리를 거칠 필요가 없으며 iris 데이터의 클래스(범주, 라벨)은 사용되지 않는다. (즉, 학습데이터와 검증데이터의 분리는 군집화에선 클래스(범주)가 없다고 가정하기에 필요없음. 텍스트, 범주형 자료의 실수화 또한 iris데이터에선 클래스(범주)에 해주는 것이기에 필요없음.)
# 필요한 라이브러리들 호출
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import load_iris # iris 데이터 로드
from scipy.cluster.hierarchy import dendrogram # 덴드로그램을 그리기 위한 라이브러리
from sklearn.cluster import AgglomerativeClustering # 계층적 군집화를 위한 라이브러리# 연결 행렬과 그에 따른 덴드로그램을 만들어주는 함수
def plot_dendrogram(model, **kwargs):
# 덴드로그램을 위해 각 노드의 아래의 자식노드들을 count해주는 과정
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
# 위에서 계산된 것을 바탕으로 덴드로그램의 바탕이 되는 연결 행렬 생성
linkage_matrix = np.column_stack(
[model.children_, model.distances_, counts]
).astype(float)
# 그에 따른 덴드로그램 생성
dendrogram(linkage_matrix, **kwargs)X = load_iris().data # 데이터 로드. Y(목표값)은 생성하지 않음 -> 비지도학습
model = AgglomerativeClustering(distance_threshold=0, n_clusters=None) # 계층적 군집화 선언
# 전체 트리(덴드로그램)을 만들기 위해 distance_threshold(거리 임계값)를 0으로 설정
# 계층적 군집화는 덴드로그램 생성 후에 군집의 개수를 설정할 수 있음 -> n_clusters=None
model = model.fit(X) # Y(목표값)을 사용하지 않고 X(입력값)만을 사용하여 군집화 실행
# 덴드로그램 생성
plt.title("Hierarchical Clustering Dendrogram")
# plot the top three levels of the dendrogram
plot_dendrogram(model, truncate_mode="level", p=3)
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.show()
이렇게 덴드로그램이 형성되면 우린 원하는 군집의 개수로 이들을 나눌 수 있다. iris데이터의 클래스가 4개이기에 군집의 개수를 4로 설정하고 싶다면 유사도가 5에서 10사이인 구간에서 자르면 된다. 이렇게 계층적 군집화는 군집을 미리 설정하지 않고 군집의 결과를 통해 선택할 수 있다.
2) 분리형 군집화(K-means)
분리형 군집화는 이해하기 쉽게 데이터를 생성하여 실습을 진행하였다.
import matplotlib.pyplot as plt # 시각화 도구
from sklearn.datasets import make_blobs # 가상 데이터 생성을 위한 라이브러리 호출
X, Y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 4개의 군집을 가진 300개의 smaple을 생성
plt.scatter(X[:,0], X[:,1], c=Y) # 그래프로 시각화
모든 방향으로 같은 성질을 가지는 정규분포를 이용해 가상 데이터를 생성한 결과이다. 적절한 군집화를 위해 일단 4개의 군집을 가지게 설정하였다. 위의 코드에서 Y를 준 이유는 단지 시각화를 통해 군집의 올바른 결과를 보여주기 위해서 이다. (즉, 군집화의 학습에 사용되지 않는다.)
from sklearn.cluster import KMeans # 분리형 군집화 호출
kmeans = KMeans(n_clusters=4, random_state=0) # 군집은 4개로 학습 전 설정해주어야 함.
kmeans.fit(X) # 군집화 실행이론에서 봤듯이 분리형 군집화는 군집을 위해 미리 군집의 개수를 설정해야된다. 물론 적절한 군집의 수를 구하기 위해선 Elbow point를 찾는 등 다양한 방법을 사용해야 하지만, 여기선 간단한 가상 데이터이기에 따로 측정하진 않는다. 또한, 앞서 말한 것처럼 군집화는 비지도학습이기에 미리 설정했던 Y값은 군집화에 사용되지 않는다.
Y_pred = kmeans.predict(X) # 군집의 결과
plt.scatter(X[:,0], X[:,1], c=Y_pred) # 군집의 결과 출력
centers = kmeans.cluster_centers_ # 각 군집의 중심
plt.scatter(centers[:, 0], centers[:,1], c='Red', s=200, alpha=0.4) # 각 군집의 중심 출력

위에서 봤던 군집의 결과와 똑같이 잘 나왔다. 하지만 여기서 의문일 수 있는 것은 각 군집의 색깔이 기존에 설정한 색깔들과 다르게 나왔다는 점이다. 그렇다면 군집이 잘 안되었다는 뜻일까? 아니다. 군집의 색깔을 맞추는 것은 분류에서의 문제이다. 군집은 그저 어떤 클래스이건 비슷한 데이터끼리 묶는 것에만 집중한다. 이 점이 분류와 군집의 큰 차이 중 하나이기도 하다.
이번엔 초승달 모양 클러스터 두 개 형상의 데이터를 생성하고 군집화를 진행해보자. 분리형 군집화는 이 데이터의 모양을 잘 군집할 수 있을까?
from sklearn.datasets import make_moons # 가상 데이터 생성에 필요한 라이브러리
import matplotlib.pyplot as plt
X,Y = make_moons(n_samples=200, noise=.05, random_state=0) # 가상 데이터 생성 (초승달 모양)
plt.scatter(X[:,0],X[:,1], c=Y) # 시각화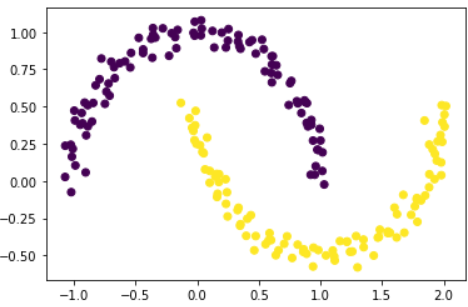
Y_pred = kmeans.predict(X) # 군집화를 통한 예측
plt.scatter(X[:,0], X[:,1],c=Y_pred) # 시각화
당연히 잘 안된다. 이론에서 말했듯이 분리형 군집화는 지역적 패턴이 존재하는 군집을 판별하는 데에 부족함을 보인다. 그래서 이런 데이터에는 분포 기반 군집화(DBSCAN)이 필요한 것이다.
3) 분포 기반 군집화(DBSCAN)
앞선 가상 데이터를 분포 기반 군집화로 풀어보자.
from sklearn.cluster import DBSCAN # 분포 기반 군집화 DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=5, metric='euclidean') # e = 0.2, M = 5
# eps: e-neighborhood / min_smaples: M -> 실험적으로 선정 필요
Y_pred = dbscan.fit_predict(X) # 군집화 진행 및 결과
plt.scatter(X[:,0], X[:,1],c=Y_pred) # 시각화
DBSCAN을 통해 지역적 패턴을 가지고 있는 데이터에 대해 정확한 군집이 이루어진 것을 확인할 수 있다.
'공부 > 기계학습 및 인공지능' 카테고리의 다른 글
| Machine Learning (기계학습) - part 9 [교차 검증, 모델 최적화, 파이프라인] (0) | 2022.01.16 |
|---|---|
| Machine Learning (기계학습) - part 8 [차원축소, 주성분 분석(PCA)] (0) | 2022.01.15 |
| Machine Learning (기계학습) - part 6 [SVM (Support Vector Machine)] (0) | 2022.01.12 |
| Machine Learning (기계학습) - part 5 [의사결정나무(Decision Tree)] (0) | 2022.01.11 |
| Machine Learning (기계학습) - part 4 [판별분석(Discriminant Analysis)] (0) | 2022.01.09 |