2021년도에 대학교 과목으로 들었던 '기계학습' 강의를 복습 및 정리 + 추가적인 공부를 위해 이 글을 작성한다. (세종대학교 최유경 교수님 '2021 기계학습'수업)
저번 파트에 이어서 이번에도 지도학습의 학습 모델 중 의사결정나무(Decision Tree)에 대해 알아본다.
의사결정나무(Decision Tree)는 이전 파트에 배웠던 학습 모델들과는 같이 예측 모델을 만들고 이 모델의 파라미터를 추정하여 예측을 진행하지 않고 특정 알고리즘을 통해 학습 및 예측을 진행한다. 의사결정나무같은 경우 최근에 자주 사용되는 다양한 앙상블 머신러닝 기법의 기반이기에 좀 더 확실히 인지하고 갈 필요가 있다.
의사결정나무(Decision Tree)
이론
의사결정나무란 무엇일까? 의사결정나무란 학습 데이터 자체를 분석하여 데이터에 내재되어 있는 패턴을 통해 새롭게 관측된 데이터를 예측 및 분류하는 모델이다. 개념적으로 생각해보면 질문을 던져서 대상을 좁혀 나가는 '스무고개 놀이'와 비슷하다고 할 수 있다. 즉, 목적(Y)과 자료(X)에 따라 적절한 분리 기준과 정지 규칙을 지정하여 하나의 의사를 결정하는 Tree를 생성하는 것이다. 이러한 결정 방식 과정을 나타낸 모델이 나무와 같다고 하여 의사결정나무라고 불리게 된 것이다.
그럼 수무고개를 통해 의사결정나무의 결정 방식에 대해 간단히 이해해보자.

우리가 찾고자 하는 대상이 '호랑이'라고 했을 때, 가장 먼저 분리되는 기준을 '다리의 유무'로 설정했다고 해보자. 호랑이는 다리가 있기에 왼쪽으로 이동하여 다시 '크기 비교'라는 새로운 분리 기준을 만나게 된다. 이렇게 여러가지의 분리 기준과 '해당 범주에 속하는 생물의 최소 개수'라는 정지 규칙을 통해 결론적으로 우린 호랑이를 찾아낼 수 있다. 이게 바로 의사결정나무가 결정되는 과정인 것이다.
이런 의사결정나무를 활용한 데이터 분석은 어떻게 진행 될까? 먼저 다변량 변수(범주가 2개 이상인 변수)인 데이터를 사용하여 한번에 설명 변수 하나씩 데이터를 2개 혹은 그 이상의 부분집합으로 분할한다. 즉, 설명 변수가 분리 기준이 되는 것이다. 그 후 데이터 순도가 균일(비슷한 범주만이 남은 상태)해질때까지 재귀적 분할을 통해 데이터를 반복하여 분리하게 된다. 결론적으로 분류 문제에서는 끝 노드에 비슷한 범주(클래스)를 갖고 있는 관측데이터끼리 남은 경우, 예측 문제에서는 비슷한 수치(연속된 값)를 갖고 있는 관측데이터끼리 남을 경우 재귀적 분할 즉, 의사결정과정은 종료된다. 이런 학습과정을 거쳐 결정된 의사결정나무를 통해 우린 새로운 데이터를 (분류라면 결론적으로 도달한 그 끝 노드에서 가장 빈도가 높은 범주로, 회귀라면 그 끝 노드의 평균을 통해) 추론하게 되는 것이다.
본격적으로 의사결정나무의 학습 알고리즘을 알아보기 전, 이 학습 모델의 장점과 단점을 알아보자.
의사결정나무는 앞서 설명한 스무고개 방식으로 표현되기 때문에 모델 자체를 쉽게 이해하고 적용할 수 있으며 이에 따라 데이터의 통계적 가정이 필요 없다. (LDA같은 경우 데이터의 정규성과 관련된 가정이 필요했음) 또한 가장 중요한 장점은 이러한 의사결정과정에 대한 설명(해석)이 가능하며 이에 따라 중요한 변수 선택에 유용하다는 것이다. 간단한 예시를 통해 이해해보자.

해당 날짜에 진행될 야구경기에 대해서 진행할 수 있을지에 대한 예측을 해본다고 가정하자. 이때 이전 기록의 데이터를 통해 학습된 의사결정나무가 있다고 할 때, 우린 이 의사결정나무를 통해 예측할 수 있을 것이다. 그렇다면 여기서 중요한 변수는 어떤 것이고 만약 취소될것이라고 예측했다면 왜 그런 결정이 나왔는지 설명할 수 있을까? 의사결정나무라면 가능하다. 가장 중요한 변수는 해당 나무가 알고리즘을 통해 결정한 가장 상단의 설명변수(스무고개의 첫번째 질문)일 것이다. 또한 취소될것이라고 예측했다면 우린 해당 나무의 분류 기준들을 차근차근 거쳐가며 이유를 설명할 수 있을 것이다. 이런 부분이 바로 의사결정나무의 가장 큰 장점이라고 할 수 있다.
하지만 의사결정나무도 단점은 존재한다. 좋은 모형(나무)를 만들기 위해선 많은 데이터가 필요하며 상대적으로 시간이 많이 소요된다. 또한, 데이터의 변화에 유독 민감하기도 하다. 그래서 학습데이터와 검증데이터의 도메인 갭이 작아야 한다는 가정을 품고 있다. 또한 선형 구조형 데이터에 취약하다는 단점도 있다.
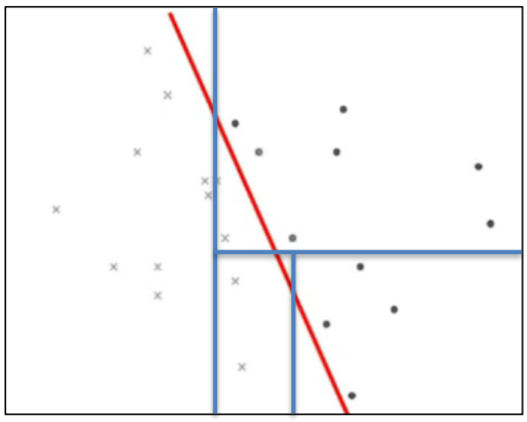
예를 들어 이렇게 선형 구조를 가지고 있는 데이터를 분리한다고 하자. 이럴 땐 사실 의사결정나무보다는 선형 분리가 가능한 다른 학습 모델이 예측에 더 좋은 성과를 낼 것이다.
마지막으로 '과적합'이라는 가장 큰 단점이 존재한다. 의사결정나무에서의 과적합은 끝 없는 분할의 결과라고 볼 수 있다. 즉, 학습용 데이터를 끝없이 분할하면서 잡음(노이스)이 포함될 수도 있는 학습용 데이터에만 완전히 적합되게 된다. 이런 결과로 검증데이터에서의 오차는 일반적으로 증가하게 되는 것이다.

이런 큰 단점을 개선하기 위해선 의사결정나무에선 나무의 성장을 중단하는 성장 멈추기, 가지치기 2가지 과적합 방지 기법을 사용한다.
1. 성장 멈추기(Stop condition)
성장멈추기는 나무 모델의 깊이 혹은 관측치 수에 제한을 두는 것이다. 즉, 나무 모델을 성장시키다가 해당 제한 조건에서 성장을 중단시키는 것이다. 이는 CHAID 알고리즘에서 사용하는 방법이기도 하다.
2. 가지치기(Pruning)
가지치기는 한마디로 '다해보고 결정하자!'라고 표현할 수 있다. 즉, 완전히 나무 모형을 생성한 후 필요없는 가지들을 자르는 방식이라고 생각하면 된다. 이는 가지치기 비용함수를 최소로 하는 분기를 찾음으로써 수행한다. 근데 여기서 자른다고 하면 그 가지에 대한 데이터를 버리는 것이라고 생각할 수 있지만 사실 합치는 개념이다. 이는 성장 멈추기(Stop condition)보다 성능이 우수하다고 알려져 있다.


이제 본격적으로 의사결정나무가 어떤 방식으로 학습이 진행되는지, 사용되는 학습 알고리즘들을 살펴보며 이해해보자. 기본적으로 사용되는 알고리즘(재귀적 분할 알고리즘)은 CART(Classification And Regression Tree), C4.5, CHAID(Chi-square Automatic Interaction Detection)이 있다. 이때 의사결정나무는 분류 나무(목표값이 범주형)냐 회귀 나무(목표값이 수치형)냐에 따라 사용되는 알고리즘은 다르다. 그럼 먼저 분류 나무와 회귀 나무의 차이를 알아본 후 각각의 나무에 따라 어떤 알고리즘이 사용되는지 살펴보자.
1. 분류 나무
계속 배워 왔던 것과 같이 분류나무는 범주형 변수를 분리하는 데에 사용되며 분류 결과를 판별과 추론 두가지로 반환하게 된다. 즉, 소속 집단에 대한 판단과 그에 따른 경향성도 확률로 표현이 가능하다는 것이다.
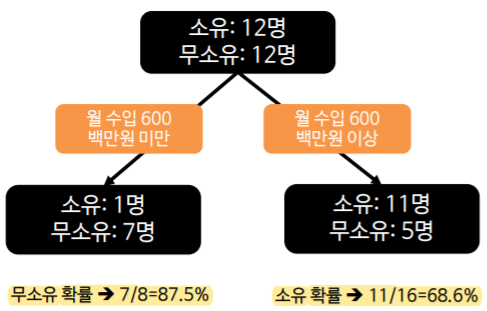
이런 분류나무에는 위에서 언급한 모든 알고리즘이 사용될 수 있다.
2. 회귀 나무
회귀 나무 또한 배워왔던대로 수치형 변수를 예측하는데 사용된다. 회귀나무는 끝 마디 집단의 평균을 통해 예측을 진행한다. 하지만 회귀같은 경우 보통 회귀나무보다 앙상블 모델, 신경망 또는 앞서 배운 회귀분석이 더 좋은 결과를 내긴 한다.

또한 이 알고리즘들은 이진 분할이냐 다중 분할이냐에 따라 나뉘기도 한다.
[이진분할(binary split): CART / 가지가 2개]
[다중분할(multi-way split): CHAID, C4.5 etc / 가지가 2개 이상]
이제 본격적으로 각각의 알고리즘(재귀적 분할 알고리즘)이 어떻게 동작하는지 알아보자
1. CART (Classification & Regression Tree)
CART는 이름에서 알 수 있듯이 분류나무, 회귀나무에 모두 사용 가능하며 이진 분할 방법을 사용하여 분리기준을 세운다. 또한 과적합 방지를 위해 가지치기를 사용하는데, 이때 중요한 것은 학습 데이터로 나무를 생성한 후 그 학습 데이터가 아닌 검증 데이터로 가지치기를 진행한다는 것이다. 이는 교차 검증을 통해 이루어진다. (교차 검증은 추후에 자세히 설명)
1) 분류
분류로써 사용되는 CART의 불순도 알고리즘(분할 기준 측정)은 지니 지수(Gini index)를 사용하고 해당 지니 지수(불확실성을 표현)가 낮아지는 기준을 더 좋은 기준이라고 판단한다.
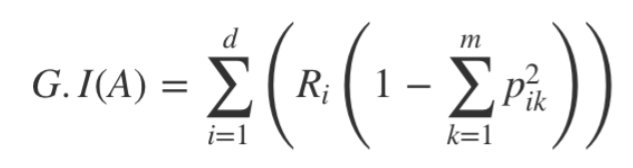
예시를 통해 지니지수를 통해 어떻게 분류 기준을 찾는지 자세히 알아보자.
홈쇼핑에서 충성 고객과 탈퇴 고객을 구분하는 규칙(의사결정나무)을 생성한다고 가정해보자. 총 10명의 고객을 대상으로 성별, 결혼유무 중 어느 변수가 더 분류를 잘하는 변수인지 찾고 그에 따른 분류 규칙을 찾는 것을 목적으로 한다고 생각하자. 이 과정이 결국 불순도 알고리즘(Gini Index)을 통해 더 좋은 기준을 찾는 과정이라고 할 수 있다.

위에서 설명한 지니 지수의 수식을 그대로 이용하면 어떤 변수가 분류를 더 잘하는지 바로 판단이 가능하다. 먼저, 성별에 의해 분류를 진행했을 경우 해당 수식을 통해 나온 결과는 0.167이다. 그 다음으로 결혼유무에 의한 분류를 진행했을 경우 수식을 통해 0.48이라는 결과를 얻을 수 있다. 앞서 말한 것처럼 지니 지수는 불확실성에 대한 수치라고 했다. 그러므로 둘중 더 작은 지니 지수(불확실성)를 갖는 '성별'이 더 좋은 분류 기준이 된다고 할 수 있는 것이다. 이는 분류 결과를 통해서도 알 수 있는 사실이다.
2) 회귀
회귀에서의 CART의 알고리즘은 분류와 불순도 측정 방법, 성능 평가 방법의 차이를 보인다. 회귀에서의 CSRT는 분류(지니 지수)와 다르게 제곱 오차 합(SSE, the Sum of the Squaured Errors)을 이용하여 불순도를 측정한다. [오차 = 실제값 - 예측값]

즉, 이 SSE가 작은 기준을 더 좋은 기준으로 평가한다는 말이다.
그리고 성능 평가 방법(예측모델 평가 방법)은 이를 이용한 RMSE(평균 제곱근 편차)를 사용한다. 평균 제곱근 편차는 말 그대로 제곱 오차 합(SSE)의 평균에 제곱근을 씌운 형태이다.

앞서 말했듯이 회귀문제는 의사결정나무를 통해 해결하는 것보다 앙상블 모델, 신경망 또는 앞서 배운 회귀분석이 더 좋은 결과를 보이기에 자주 사용되는 추세는 아니다.
2. C4.5
C4.5 또한 분류 나무와 회귀 나무에 모두 사용된다. 하지만 CART와는 다르게 다중 분할을 통해 분리를 진행하며 가지치기는 학습 데이터만을 이용하여 수행한다. 즉, CART와는 다르게 나무 성장과 가지치기 모두에 학습데이터만을 이용한다는 것이다. 불순도 알고리즘은 엔트로피를 사용한 정보이론, 정보이론 이득률을 통해 수행된다.

해당 식 즉, 정보이론(엔트로피(E: Entropy))에서 -log를 사용하는 이유는 log를 통해 bit 수로 정보를 계산하고 확률에 로그를 취하는 것이므로 -를 +로 전환하기 위해 log앞에 -를 붙여준다고 생각하면 된다. 또한, 정보 이익(IG: Infromation Gain)이란, 정보의 가치를 측정하는 방법이다. 이는 불확실성의 차이를 통해 계산된다 [IG = E(before)-E(after)] 높을 수록 정보의 개선이 있다고 판단한다.(즉, 높을 수록 좋은 분류 기준)
그럼 앞선 예시를 통해 이 C4.5이 어떻게 불순도 알고리즘을 통해 더 좋은 분류 기준(특성)을 찾는지 더 깊게 알아보자.

다시 상기시키자면 정보 이득은 Root노드의 엔트로피(불확실성)과 해당 기준을 통해 나온 결과의 엔트로피(불확실성)의 차이이다. 즉, 불확실성이 해당 분리 기준(변수)를 통해 얼만큼 개선되었냐를 판별하는 것이다. 그럼 이제 예시의 결과를 보자. 두 변수(분리 기준) 중 정보 이익이 큰 변수는 성별이다. 즉, 성별이 더 좋은 분류 기준이 된다고 말할 수 있는 것이다. 이는 앞선 CART와 같은 결과이다.
하지만, 이 정보 이득만을 따지게 되면 생기는 아주 큰 문제가 하나있다. 바로, 가지수가 많으면 많을 수록 IG가 높아지는 경향을 보인다는 문제이다. 이는 가짓수가 많은 다중 분할에서 흔히 볼 수 있는 문제이다. 이를 해결하기 위해서 나오는 개념이 바로 '정보이론 이득률(information gain ratio)'이다. 즉, 단점을 보안하기 위해 IV(Intrinsic Value)를 도입하여 정보 이득을 정규화 한 것이다. (가지 수에 대해 감점을 반영)



물론 현재 예시가 간단한 수식을 설명하기 위해 이진 분할이여서 IV를 반영한 효과를 보지 못하고 있지만, 이진 분할을 다중 분할로 바꾼다면 -log2()가 계속 붙게되어 IV가 1을 넘어 정규화가 이루어지는 것을 확인할 수 있다.
3. CHAID(CHi-square Automatic Interaction Detection)
CHAID는 위에서 설명한 알고리즘들 중 가장 오래된 재귀적 분할 알고리즘이다. CHAID에서는 더 좋은 분류 기준을 찾기 위해 카이제곱(Chi-square)을 이용한다. (높을 수록 더 좋은 분류 기준)
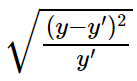
CHAID는 앞선 알고리즘들과는 다르게 회귀에 적용하지 못한다는 특징이 있으며 추가적인 과적합 방지 기법을 사용하지 않고 나무 성장 시에 최적의 모형을 개발한다는 특징이 있다. 즉, 과적합이 되기 전에 나무 성장을 멈춘다는 뜻이다.
CHIAD는 C4.5과 마찬가지로 전체 자료를 둘 이상으로 반복적으로 분할(다중 분할)한다. 이 과정에서 설명변수의 범주의 쌍에 대한 목표값(Y)의 유의한 차이가 없으면 설명변수의 범주들을 합치고 유의적이지 않은 쌍들이 없을 때까지 과정을 계속하여 성장과 동시에 과적합을 방지한다. 즉, 나무를 형성을 하며 각 설명변수에 대한 최고의 분할을 찾고, 모든 설명변수에 대한 유의성을 조사하여 가장 유의적인 설명변수(분리를 잘하는)를 선택한다. 선택된 설명변수의 범주들의 그룹을 사용해 자료를 상호 배반인 부분집합으로 분할하고 각 부분집합에서 정지규칙중의 하나가 만족될 때까지 이 과정을 순환, 반복한다.
지금까지 설명한 재귀적 분할 알고리즘을 정리한 표이다. 이를 통해 설명했던 알고리즘을 다시 상기시켜 보자.

실습
1. 분류(Classification)
분류는 이전 part1에서 사용했던 iris데이터를 사용한다. [참고]
(이전에 진행했던 부분이기에 자세한 설명은 생략)
# 데이터 로드 및 데이터 분리(input, output)
import seaborn as sns
iris = sns.load_dataset('iris') # iris data
x = iris.drop('species',axis=1) # input
y = iris['species'] # output
iris.head(3)
# 텍스트 및 범주형 자료 실수화
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
new_y = le.fit_transform(y)
set(new_y) # -> {0, 1, 2}# 학습데이터 및 검증데이터 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = \
train_test_split(x,new_y, test_size=0.3, random_state=11, stratify=new_y)
print('Train :',x_train.shape) # -> Train : (105, 4)
print('Test :',x_test.shape) # -> Test : (45, 4)마지막으로 이제 전처리가 완료된 데이터를 통해 의사결정나무 모델을 학습시키자
# 의사결정나무를 통한 학습 진행
from sklearn.tree import DecisionTreeClassifier
DT1 = DecisionTreeClassifier(criterion='gini', max_depth=5, random_state=1) # CART 의사결정나무
DT2 = DecisionTreeClassifier(criterion='entropy', max_depth=5, random_state=1) # C4.5 의사결정나무
dt1 = DT1.fit(x_train, y_train) # CART 학습 진행
dt2 = DT2.fit(x_train, y_train) # C4.5 학습 진행여기서 중요한 부분은 바로 criterion과 max_depth라는 인자 설정 부분이다.
criterion은 이론에서 배운 불순도 알고리즘을 선택할 수 있는 인자이다. criterion을 'gini'로 선택할 경우 gini index(지니 지수)를 통해 더 좋은 분류 기준을 선택하게 된다. 즉, CART 재귀적 분할 알고리즘을 통한 의사결정나무가 생성된다는 것이다. criterion을 'entropy'로 설정할 경우 엔트로피 및 정보 이득률(infromation gain ratio)을 통해 더 좋은 분류 기준을 선택하게 된다. 즉, C4.5 재귀적 분할 알고리즘을 통한 의사결정나무가 생성된다는 것이다.
max_depth는 말 그대로 최대 깊이이다. 이는 앞에서 배운 이론 중 과적합 방지의 가지치기에 해당한다. 즉, max_depth를 5로 설정했다는 것은 학습시키는 나무에 대해 완전히 성장시킨 후 깊이가 5이상 넘어가지 않도록 가지를 자른다(데이터 통합)고 생각하면 된다.
이 둘의 인자 또한, 이전 실습에서 진행했던 학습 모델의 하이퍼 파라미터와 같이 정해진 정답이 없고 모두 실험적으로 접근하여 최적의 하이퍼 파라미터를 구해야 한다.
# 예측 정확도 (accuracy score)
print(DT1.score(x_test, y_test)) # 0.9777777777777777
print(DT2.score(x_test, y_test)) # 0.9555555555555556이 iris 데이터에서는 지니 지수를 이용한 CART 알고리즘이 더 좋은 성능을 보이는 것을 확인할 수 있다.
마지막으로 생성된 의사결정나무를 출력해보자. 이 부분은 앞서 말했던 의사결정나무의 가장 큰 장점인 '의사결정과정에 대한 설명(해석)이 가능하며 이에 따라 중요한 변수 선택이 가능하다'의 부분이다. 그래프를 통해 우린 어떻게 의사결정이 이루어졌고, 어떤 변수가 중요한 변수로 판단되었는지 확인이 가능하며, 그에 따른 각 변수에 대한 불순도 수치 또한 확인할 수 있다.
# 학습된 의사결정나무 그래프를 통해 출력
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree # 트리를 그리게 해주는 도구
fig,ax = plt.subplots(figsize=(25,12)) # 그래프 크기 설정
plot_tree(dt1, fontsize=15) # 트리 출력
해당 그래프를 통해서 우린 주어진 설명변수 중 인덱스가 3인 변수가 가장 중요한 변수라는 것을 알 수 있다. 또한, 어떤 변수와 그에 따른 어떤 기준으로 데이터들이 분류되었는지 확인이 가능하다. 이게 바로 의사결정나무의 가장 큰 장점이다.
2. 회귀(Regression)
다음은 회귀에서의 의사결정나무를 확인해보자.
회귀 예측을 위해 sin형태를 가지지만, 중간 중간에 노이스가 낀 랜덤한 데이터를 생성하고 이에 대해 학습하여 의사결정나무의 max_depth에 따른 과적합에 대해 알아보자.
# 랜덤한 회귀 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0) #0~5 사이의 랜덤한 실수 데이터
y = np.sin(X).ravel() # 예측을 위해 sin 형태를 가지는 y라벨 생성
y[::5] += 3 * (0.5 - rng.rand(16)) # 중간 중간에 noise 생성
# 그래프를 통해 데이터 확인
plt.figure()
plt.scatter(X, y, s=40, edgecolor="black", c="darkorange", label="data")
plt.xlabel("data")
plt.ylabel("target")
plt.legend()
plt.show()
# 의사결정나무를 통해 회귀 진행
from sklearn.tree import DecisionTreeRegressor # 회귀용 의사결정나무 호출
reg1 = DecisionTreeRegressor(max_depth=2) # 과적합 우려X // criterion='mse'
reg2 = DecisionTreeRegressor(max_depth=5) # 과적합 우려O // criterion='mse'
reg1.fit(X, y) # 학습 진행
reg2.fit(X, y) # 학습 진행회귀 또한 앞선 분류에서 봤듯이 criterion이라는 불순도 알고리즘을 선택하는 인자와 max_depth가 존재한다. criterion은 이론에서 살펴봤듯이 mse를 대표적으로 많이 쓰기에 애초에 mse가 초깃값으로 설정되어 있다. 그렇다면 우리가 중요하게 볼 부분은 max_depth이다. 여기서 max_depth를 2와 5로 두어 가지치기를 많이하냐 안하냐(과적합 방지의 정도)의 차이를 확인해보려한다. (max_depth=5 가 과적합 방지의 정도가 적음 -> 과적합 우려)
# 예측 결과 확인
from sklearn.metrics import mean_squared_error # 평가 척도로 MSE 사용
y_pred1 = reg1.predict(X) # reg1 예측
y_pred2 = reg2.predict(X) # reg2 에측
print(mean_squared_error(y, y_pred1)) # MSE 평가 -> 0.12967126328231798
print(mean_squared_error(y, y_pred2)) # MSE 평가 -> 0.025236948989861896max_depth를 5로 둔 reg2가 학습데이터에 대해선 더 좋은 평가(더 낮은 mse(오차))를 보이고 있다. 그렇다면 이 reg2가 더 좋은 모델로 새로운 데이터에 대한 예측이 잘 이루어질까? 그래프를 통해 확인해보자.
# 예측 결과 시각화 (reg1 <- max_depth=2, 과적합 우려X)
plt.figure()
plt.scatter(X, y, s=40, edgecolor="black", c="darkorange", label="data")
plt.plot(X, y_pred1, color="cornflowerblue", label="reg1_pred", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
파란색 선 그래프가 학습된 reg1의 예측 결과이다. max_depth=2의 reg1은 모든 학습데이터에 대해 정확히 예측해내지는 못하지만, 데이터의 패턴이 sin형태인 것을 파악해 내었다. 즉, 노이즈에 영향을 받지 않고 과적합되지 않아 새로운 데이터에 대해 sin형태로 예측을 해내어 일반화에 좋은 모습을 볼 수 있는 것이다. (학습 목표는 sin형 예측을 할 수 있는 모델)
# 예측 결과 시각화 (reg2 <- max_depth=5, 과적합 우려O)
plt.figure()
plt.scatter(X, y, s=40, edgecolor="black", c="darkorange", label="data")
plt.plot(X, y_pred2, color="yellowgreen", label="reg2_pred", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
초록색 선 그래프가 학습된 reg2의 예측 결과이다. 그래프를 통해 reg2는 세부적인 결과까지 예측이 가능해졌다는 것을 볼 수 있다. 그럼 reg2가 좋은 예측 모델이라는 것일까? 아니다. 세부적인 결과까지 예측이 가능해졌다는 것은 다시 생각해보면 '노이즈'까지 학습했다는 것이다. 즉, 너무 학습데이터에만 집중하여 학습하다 보니 일반화 능력이 떨어져, 학습에 이용되지 않은 새로운 데이터에 대하여 예측할 때, 노이즈의 결과처럼 예측할 수도 있다는 것이다. 이처럼 의사결정나무를 이용할 때는 내가 사용할 불순도 알고리즘이 무엇인지, 과적합을 방지하기 위해선 얼만큼의 가지치기를 진행할지 적절한 선택을 요구한다. (실험적으로 선택해야 됨!)
지금까지 의사나무결정가 무엇인지, 의사결정나무에서 사용되는 대표적인 재귀적 분할 알고리즘은 어떤 것이 있는지 알아보았다. 서론에서 말했듯이 의사결정나무는 최근 자주 사용되는 앙상블(Ensemble, Random Forest와 Boosted Trees 등) 중 Random Forest의 기반이 되는 학습 모델이라고 했다. 이 앙상블에 대해선 추후에 자세히 다룰 예정이지만, 의사결정나무가 나온 김에 간단히 알아보고 넘어가 보자.
앙상블(Ensemble)
앙상블이란, '여러 모델을 함께 사용하자!'라는 아이디어에서 나온 개념이다. 기본적으로는 의사결정나무(Decision Tree), KNN(k-Nearest Neighbor), LDA(Linear D Analysis), 로지스틱 회귀(Logistic Regression) 등 여러 학습 모델을 동시에 사용하여 각각의 모델이 예측한 결과 중 가장 많이 나온 결과를 최종 예측으로 사용한다는 개념이다. 즉, 여러 예측 알고리즘을 조합하여 예측 성능을 향상시키는 것에 목적을 둔다. 이에 따라 앞선 일반적인 의사결정나무와는 다르게 설명보다는 예측 성능이 더 중요할 경우에 사용된다 (여러 다양한 예측 모델을 사용하므로 설명이 힘듦). 의사결정나무 파트에서 굳이 앙상블 모델을 언급하는 이유는, 이 앙상블 모델들 중 최근에 주목 받고 자주 사용되는 Random Forest, Boosted Trees 가 의사결정나무를 기반으로 만들어졌기 때문이다. 이후 파트에서 이들에 대해 자세히 다룰 예정이므로 이번 파트에선 Random Forest만을 간단히 설명하고 넘어가려 한다.
Random Forest
이론

Random Forest(랜덤 숲)은 데이터로부터 복원 추출(뽑은 표본 원복)을 이용하여 여러 샘플을 추출하는 Bootstrap을 사용하고 무작위로 예측 변수를 선택하여 모델을 구축하여 Forest(숲)을 생성한다 (의사결정나무에서는 기준 지표(불순도 알고리즘)를 사용). 이렇게 구축한 앙상블의 결과는 분류에선 각각의 tree들이 예측한 결과들 중 가장 많이 나온 결과를 최종 예측 결과로 선택하는 투표를 통해 산출되고 회귀에선 각각의 tree들이 예측한 수치를 평균내어 최종 예측 결과로 선택하는 평균화를 통해 산출된다. 결국 random forest는 기존 의사결정나무보다 더 좋은 결과를 얻을 수 있다는 장점이 생겼지만, 숲이 되면서 해석 가능한 모델의 장점은 사라졌다. (But, 결과 분석을 통해 설명 변수 중 중요한 변수를 판별할 수는 있음)
실습
randomforest 실습도 이론에서처럼 기본적으로 의사결정나무가 여러 개가 사용된다는 점을 제외하고는 의사결정나무 실습과 크게 다를 바 없다. 실습은 iris 데이터를 그대로 사용하였다.
# randomforest를 통한 iris 데이터 학습
from sklearn.ensemble import RandomForestClassifier # randomforest 호출
rfc = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=0)
rfc.fit(x_train, y_train) # 학습 진행max_depth는 의사결정나무에서의 실습과 똑같은 의미를 갖는다. 그럼 여기서 중요한 부분은 바로 n_estimators이다. n_estimators는 몇개의 나무모델들을 사용할 것인지를 설정하는 인자이다. 위의 예시처럼 100개를 사용한다면 학습 시 100개의 나무를 생성하고 예측 시 해당 100개의 나무들의 예측 결과 중 가장 많은 표가 나온 예측을 최종 예측 결과로 사용한다.
# 성능 평가 (accuracy score)
rfc.score(x_test, y_test) # 0.9777777777777777