Machine Learning (기계학습) - part 8 [차원축소, 주성분 분석(PCA)]

snn.il 2022. 1. 15. 23:11

2021년도에 대학교 과목으로 들었던 '기계학습' 강의를 복습 및 정리 + 추가적인 공부를 위해 이 글을 작성한다. (세종대학교 최유경 교수님 '2021 기계학습'수업)

저번 파트는 비지도학습(Unsupervised learning)의 군집화에 대해 알아보았다. 이번 파트에는 비지도학습의 또 다른 방법인 변환(Transform)의 차원축소(주성분 분석 : PCA)에 대해 알아보자. [변환(Transform): 데이터를 새롭게 표현하여 사람이나 학습 모델이 원래 데이터보다 쉽게 해석할 수 있도록 만드는 것]

차원축소

차원축소는 일반적으로 머신러닝 알고리즘을 적용할 때 사용되기보다는 데이터의 전처리 과정에서 사용된다. 즉, 정규화, 텍스트/영상 처리 등 과 같이 머신러닝이 보다 좋은 예측을 이끌기 위해 해주는 과정인 것이다. 그렇다면 이런 차원축소는 왜 필요한 것일까?

차원 축소는 보통 차원이 저주가 발생할 가능성이 높은 고차원 데이터(High dimesional data)에서 사용된다. 즉, 차원축소는 차원의 저주를 막기위해 사용되는 것이다. 차원의 저주란, 차원이 증가할 수록 동일 정보량을 표현하기 위해 필요한 데이터의 수가 지수적으로 증가하는 것을 의미한다. 결국 고차원 데이터는 학습을 위해 차원이 증가하면서 학습 데이터 수가 차원 수보다 적어져 모델의 성능이 저하되는 현상이 일어나게 된다. 즉, 차원이 증가할 수록 개별 차원 내 학습할 데이터 수가 이전보다 적어(Sparse)지는 현상이 발생한다는 뜻이다.

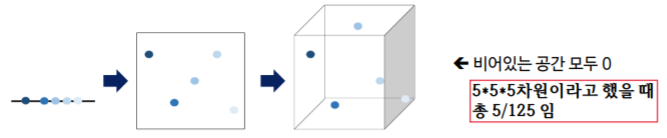
이 뿐만아니라 고차원 데이터는 차원이 높으면 높을수록 데이터에 포함될 노이즈의 비율도 높아지고 모델 학습과 추론의 계산 복잡도가 높아지는 큰 한계를 가지고 있다.

그렇다면 이런 차원의 저주를 막기위해 차원을 축소한다면 어떻게 보면 데이터의 정보를 줄이는 것과 같은데, 좋은 예측 결과가 나올 수 있을까? 결론부터 말하자면 가능하다. 일반적으로 데이터의 intrinsic dimesion(표현력을 상실하지 않을 정도의 차원)은 original dimesion(원래의 차원)보다 상대적으로 작다. 이는 MNIST 데이터를 통해서도 확인이 가능하다. MNIST는 16 X 16 의 차원(256 차원)을 가진 데이터인데 이른 차원축소를 통해 2차원 데이터로 만들어도 각 개체들에 대한 표현력이 크게 줄어들지 않는다. (추가로 축소된 차원을 원래 차원으로 복구하는 것도 어렵지 않게 진행 가능)

256차원에서 2차원으로 줄어도 대략적으로 MNIST 클래스의 형태가 유지됨

결국 이런 차원 축소는 모델의 성능을 최대로 해주는 변수의 일부 셋을 찾아 필요없는 변수는 없애주어 전체적인 데이터의 차원을 줄이는 것이다. 이를 통해 적절한 정보를 유지하면서 중복되거나 불필요한 변수를 제거할 수 있게 되는 것이다. 이런 차원 축소를 실현하는 데 사용되는 방법은 변수 선택(Feature selection), 변수 추출(Feature extraction) 2가지가 있다.

변수 선택(Feature selection)은 말 그대로 유의미한 변수만을 "선택"하는 것이다. 이는 선택한 변수에 대한 해석이 가능하다는 장점이 있지만, 변수간 상관관계를 고려하기에 어려움이 있다는 단점이 있다.

변수 추출(Feature extraction)은 예측 변수의 변환을 통해 "새로운 변수를 추출"하는 것을 말한다. 이는 변수 생성(Feature construction)이라고도 한다. 이는 선택과는 달리 변수간의 상관관계를 고려하여 변수의 개수를 많이 줄일 수 있다는 장점이 있다. 하지만, 추출된 변수가 어떤 의미를 가지는지 해석하기는 어렵다.

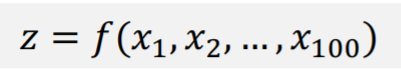
본격적인 비지도학습의 차원 축소 기술에 대해 알아보기 전 우린 이전에 차원축소가 지도학습(LDA)에서 언급됐었다는 것에 의문이 생길 수도 있다. 그럼 지도학습에서의 차원축소는 비지도학습과 동일한 방법을 사용하는 것일까? 아니다. 지도학습 기반 차원 축소(LDA에서 사용됨)는 학습결과가 피드백되어 변수 선택을 반복한다. 하지만 비지도학습 기반 차원 축소는 지도학습처럼 피드백을 받지도 않고 이에 따라 변수 선택 또한 반복하지 않는다. 그림을 통해 이해해 보자.

지도학습같은 경우 클래스(목표값)이 존재하기에 이를 바탕으로 차원축소된 결과를 평가하고 이에 대해 피드백을 주면서 반복적으로 변수 선택을 이루면서 더 좋은 변수를 선택한다. 하지만 비지도학습은 클래스(목표값)이 없기에 알고리즘 자체의 판단으로 피드백 및 반복없이 한번에 진행된다.

또한, 지도학습과 비지도학습의 차원축소는 목적부터 다르다. 비지도학습은 애초부터 차원의 저주를 피하기 위해 차원축소를 진행한다. 하지만, 지도학습의 차원축소(LDA)는 차원의 저주를 피하기 위해서가 아닌 더 좋은 분류를 위해 차원축소를 진행한다. 즉, 차원축소가 목적이 아닌 분류가 목적인 것이다.

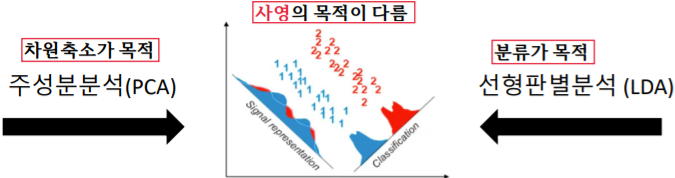
이 둘의 차이점을 알았으니 이제 본격적으로 비지도학습의 대표적인 차원 축소 기법인 주성분 분석(PCA)을 통해 차원축소가 어떻게 이루어지는 지 자세히 알아보자.

주성분 분석(PCA)

이론

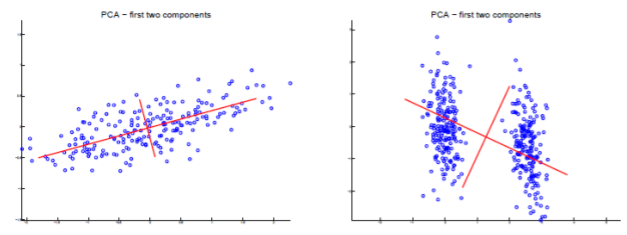
주성분 분석(PCA: Principal component analysis)은 사영 후 원 데이터의 분산(variance)을 최대한 보존할 수 있는 기저를 찾아 차원을 줄이는 방법이다. 즉, 데이터를 사영(projection, 차원의 축소 과정)시킬 경우, 손실되는 정보의 양이 적은 쪽의 기저를 선택하는 방향으로 진행된다는 것이다. 예시를 통해 확인해보자.

데이터가 주어져 있을 때, 외쪽 기저에 사영할지 오른쪽 기저에 사영할지 선택한다고 생각해보자. (둘은 똑같은 데이터를 다른 기저로 사영시키는 것) 각 그림의 하단의 결과를 통해서 우린 사영시킨 왼쪽 기저가 오른쪽 기저보다 원 데이터의 분산을 최대로 유지한다는 것을 알 수 있다. 결국 주성분 분석은 왼쪽의 기저 축을 더 좋은 기저라고 판단하고 이를 바탕으로 축소를 진행하는 것이다.

우린 이 주성분 분석의 과정을 알기 전 고유값(eigenvalue)과 고유벡터(eigenvector)와 같은 기본적인 수리적 배경이 필요가 있다.

고유벡터(eigenvector)는 그 기저에 대한 선형 변환(백터에 행렬을 곱하는 것)이 일어난 후에도 방향이 변하지 않는, 즉 0이 아닌 벡터를 말한다. 이때 고유 벡터의 길이가 변하는 배수를 선형 변환의 그 고유 벡터에 대응하는 고유값(eigenvalue)이라고 한다.

예시를 통해 보면,

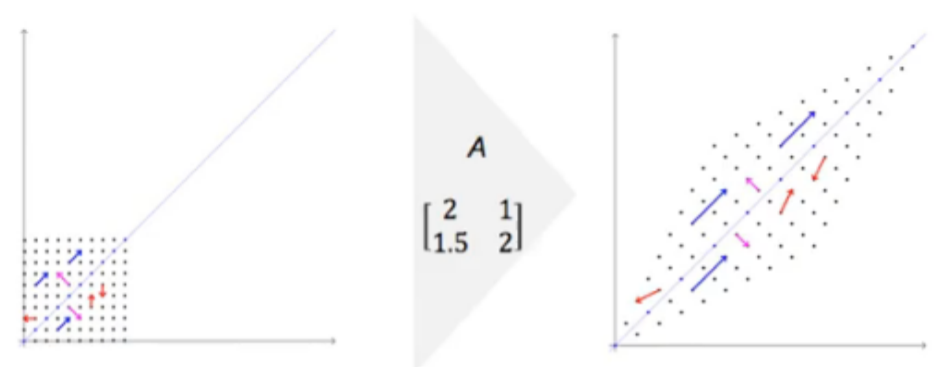
왼쪽의 벡터들에 대해 A라는 행렬을 곱해 오른쪽의 결과와 같이 선형변환을 일으킨다고 해보자. 이때 파란색의 벡터들은 방향 변화가 발생하지 않는다. 즉, 파란색 벡터들은 고유벡터에 해당하는 것이다. (고유벡터는 항상 기저에 평행한 벡터들) 여기서 파란색 벡터들이 선형변환에 의해 변환된 크기가 바로 고유값(eignevalue)인 것이다.

이제 이런 수리적 배경을 바탕으로 주성분 분석 알고리즘이 어떻게 진행되는지 살펴보자.

가장 먼저 데이터 샌터링을 진행한다. 이는 데이터의 평균을 0으로 맞추기 위해 데이터를 변경해준다. 즉, 정규화가 진행되는 것이다. (하지만 그에 따라 데이터가 가우시안 분포가 아니거나 다중 가우시안일 경우 샌터링이 불가하여 PCA 적용이 힘들다.)

이제 PCA에서의 최적화 문제를 정의한다. 우린 PCA의 목적이 사영 이후 분산 V를 최대화하는 것이라는 것을 알고 있다. 결국 최적화 문제는 분산 V를 구한 후 이를 최대로 하는 기저를 찾는 것이다. 분산은 수식으로 표현하면 밑의 모습을 보인다.

이제 이 V(분산)를 최대화하고 라그랑지 멀티플라이어(Lagrangian multiplier)를 적용하여 어떤 기저가 더 큰 분산을 가지는지 판단한다.

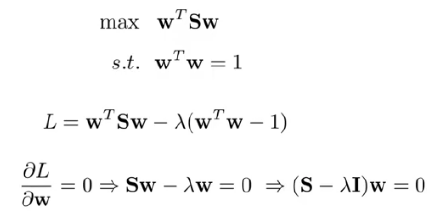
이제 이 식의 결과로 나온 고유벡터(eigenvectors, 기저들을 표현)와 고유값(eigenvalues, 분산들을 의미)을 고유값에 해당하는 고유벡터로 정렬하고 고유값(분산들을 의미)이 더 큰 고유벡터의 기저를 선택해 준다.

라그랑지 멀티플라이어의 결과/ 고유벡터는 기저를 의미. 고유값은 분산을 의미

이제 이 기저가 기존의 데이터에 비해 얼만큼 표현되어 있는지 확인하여 적절한 기저인지 판단한다. 이는 고유값의 합 중 해당 기저의 고유값의 비율로 계산된다.

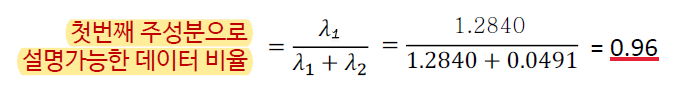
해당 결과를 통해 해당 기저를 통해 차원축소를 진행해도 원본 데이터의 96%를 설명할 수 있다는 좋은 결과가 나왔기에 해당 기저를 선택해준다.

이제 이 기저를 통해 선형 변환(결합)을 진행하여 데이터를 변환(차원 축소)하고 PCA를 마무리한다.

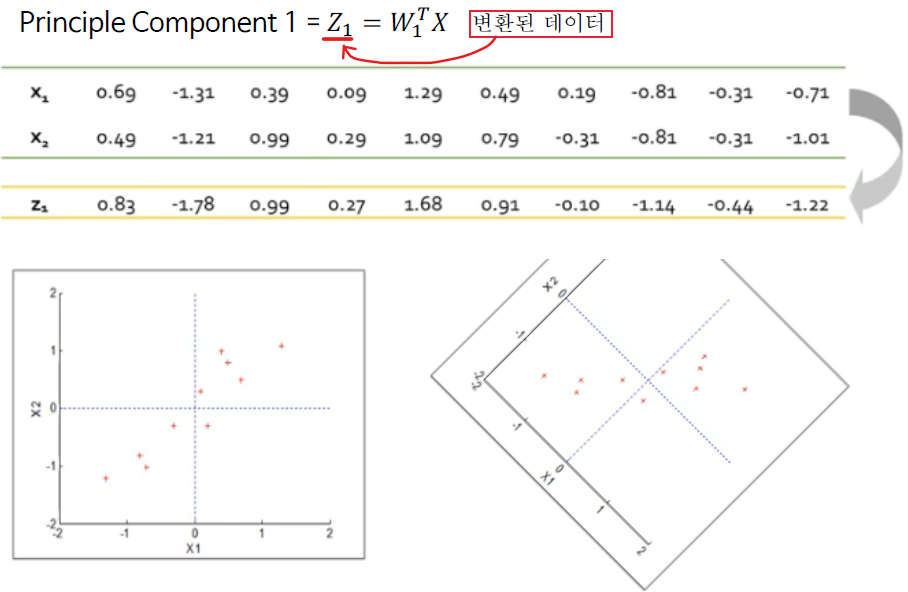
이때, 추후에 데이터를 다시 복원하고 싶다면 복원도 가능하다. 이는 앞선 과정을 역으로 진행하면 가능하다. 이게 PCA의 장점 중 하나이기도 하다. (하지만 완벽히 복원 되지는 않음)

하지만 이런 과정 속에서 문제가 되는 것은 바로 '주성분의 개수(기저의 개수)'이다. 적절한 축소를 위해 몇개의 주성분을 사용해야 되는 것일까? 이는 고유 값 감소율이 유의미하게 낮아지는 Elbow Point(군집화에서도 사용되는 개념)에 해당하는 주성분을 선택하거나 일정 수준 이상의 분산 비를 보존하는 최소의 주성분을 선택(보통 70%이상의 분산 비)하는 2가지 방법이 있다.

(1) Elbow Point 선택 / (2) 분산 비를 보존하는 최소의 주성분 선택

하지만 이런 PCA은 데이터 분포가 가우시안이 아니거나 다중 가우시안인 자료들에 대해서는 데이터 샌터링이 어려워 적용하기 어렵고 LDA와는 다르게 분류를 목적으로 차원축소가 이루어지지 않기에 분류 성능 향상을 보장하지 못한다는 두가지 한계점이 존재한다.

더 깊게 주성분 분석에 대해 알아보자면 일반적인 PCA는 자료의 크기 또는 특성변수의 크기가 매우 크면 주성분 W를 구하기 위한 계산이 불가능하거나 시간이 많이 소요된다. 이를 보완하기 위해 Randomized PCA(QR분해를 이용하여 계산 수행)를 사용하기도 한다. 또, 일반적인 PCA는 선형 변환이므로 비선형 변환에는 Kernelized PCA가 사용된다. 이는 이전에 배웠던 SVM(Support Vector Machine)의 커널트릭의 개념을 그대로 사용하는 것이다. 즉, 더 좋은 데이터 표현을 위해 변수 x를 비선형 Φ(X)_(kernel)로 변환하여 새로운 데이터 공간에서 데이터를 바라보고 이에 대해 PCA를 하여 차원 축소를 하는 방법인 것이다.

비선형 데이터를 일반적인 PCA로 차원축소한 결과와 Kernelized PCA로 차원축소한 결과

실습

이번 실습에는 이전과는 달리 특성(입력값, 차원)이 어느정도 있는 와인데이터로 실습을 진행한다. (와인 데이터는 sklearn에서 제공됨)

# 데이터 로드 및 데이터 분할(입력값, 목표값)
import pandas as pd
from sklearn.datasets import load_wine # 와인 데이터
data = load_wine()
X = data.data
Y = data.target
print(set(Y)) # {0, 1, 2}
pd.DataFrame(X).head(3)

데이터를 확인해보면 이전 iris와는 다르게 13개의 꽤 많은 특성(차원)을 가지고 있는 것을 확인할 수 있다. 물론 이대로 학습을 진행해도 큰 무리가 될 정도의 차원은 아니지만, 만약 데이터의 차원이 200,300 이라면 데이터가 많이 필요할 뿐만아니라 확실히 학습을 할 때 무리가 올 것이다. (차원의 저주)

데이터를 받아오고 데이터 전처리를 진행해준다. (학습데이터와 검증데이터로 분리한 후 데이터 정규화)

와인 데이터의 12번째 인덱스의 값을 보면 나머지 데이터들과의 스케일 차이가 심하여 정규화도 진행했다.

# 학습데이터와 검증데이터의 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X,Y, test_size=0.3, random_state=11)
print('Train set:',x_train.shape) # Train set: (124, 13)
print('Test set:', x_test.shape) # Test set: (54, 13)

# 정규화 진행
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test) # 학습데이터에 맞는 정규화 진행

이제 데이터의 차원축소를 진행한다. 하지만 몇개의 기저를 사용해야 될까? 즉, 차원을 얼만큼이나 줄여야할까? 이는 위에서 설명한 Elbow Point나 분산 비를 통해 판단해낼 수 있다.

먼저, 이를 분석하기 위해 고유벡터와 고유값을 구해준다.

##중요##
#PCA의 주축(component)개수 구하기 위한 분석
import numpy as np
cov = np.cov(x_train.T) #공분산 구하기
eigen_vals, eigen_vecs = np.linalg.eig(cov) #아이겐벨류(분산), 아이겐벡터(기저) 구하기
print('Eigenvalues \n%s' %eigen_vals)

이제 이를 바탕으로 각 기저에 따른 분산 비를 측정하여 Elbow point를 찾아 적절한 축소할 차원의 수를 선택한다.

#Explained variance ratio
total = sum(eigen_vals)
var_exp = [(i / total) for i in sorted(eigen_vals, reverse=True)] 
# 해당 주성분으로 설명가능한 데이터 비율 (분산 비)

# 기저에 따른 분산 비 시각화
import matplotlib.pyplot as plt
plt.plot(range(1,len(eigen_vals)+1),var_exp)
plt.scatter(range(1,len(eigen_vals)+1),var_exp)
plt.ylabel('Proportion of variance')
plt.xlabel('Principal component')
plt.show()

해당 결과를 통해 우린 4가 고유값 감소율이 유의미하게 낮아지는 Elbow point라는 것을 인지하고 PCA를 진행한다.

# 차원축소 - 주성분 분석(PCA) 진행
from sklearn.decomposition import PCA
pca = PCA(n_components=4) # 축소할 차원으로 Elbow point인 4로 설정
x_train_pca = pca.fit_transform(x_train) # 학습데이터에 대해 차원축소 진행
x_test_pca = pca.transform(x_test) # 검증데이터를 학습데이터 기준으로 차원축소 진행

위에서 설정한 Elbow point를 n_components(축소할 차원)로 설정하고 차원축소를 진행한다. 이때 정규화와 마찬가지로 검증데이터는 우리가 모르는 데이터라고 가정을 하기도 하고 학습데이터를 기준으로 학습된 모델을 통해 예측을 진행하기에 학습데이터 기준으로 차원축소를 진행한다.

이제 이 데이터를 바탕으로 학습 및 검증을 진행한다. (PCA를 진행하지 않은 데이터와 진행한 데이터의 예측 결과를 비교)

# 예측 진행 (로지스틱 회귀 사용)
from sklearn.linear_model import LogisticRegression

# PCA를 진행하지 않은 데이터를 통한 학습
lr1 = LogisticRegression()
lr1.fit(x_train, y_train)
print('NO PCA SCORE: \t', lr1.score(x_test, y_test))

# PCA를 진행한 데이터를 통한 학습
lr2 = LogisticRegression()
lr2.fit(x_train, y_train)
print('PCA SCORE: \t\t',lr2.score(x_test, y_test))

PCA를 진행하지 않은 데이터에 대한 예측 결과와 PCA를 진행한 데이터의 예측 결과가 차이가 나지 않았다. 즉, 이 데이터는 12차원이 아닌 4차원으로 차원을 축소해도 충분히 원 데이터를 설명이 가능하다는 뜻이다. (당연히 12차원보다 4차원으로 진행하는 것이 속도나 여러 측면에서 이득)

와인 데이터는 애초에 차원이 그리 크지 않아 이렇게 결과가 비슷하게 나오지만, 만약 고차원 데이터에 대해 PCA를 진행한다면 더 빠르고 더 좋은 예측 결과를 얻는 경우도 있다.